---

Processing日記(3)

長嶋 洋一

(一部　SuperCollider日記かも)

　Part 1　 　Part 2　 　Part 4　 　Part 5　

---

2011年4月14日(木)

前回の日記が4月5日で、もう10日ほども空いてしまった。 SuperCollider日記 の方も相当に空いてしまっていたが、新学期も、先週のガイダンスに続き、今週の3回生個別面談が今日と明日とで終われば、ぼちぼちペースが作れるかな・・・というところである。 今日は、新しくなったマルチメディア室の使い方を、佐井先生の講義の冒頭にガイダンスする予定があるぐらいなので、少しでも進めるというよりも、思い出しに重点を置きたい。

前回の続きとして、今日は チュートリアル の Trigonometry Primer I からである。 2次元平面上の任意の点の座標を、これまではxとyの直交座標系で扱ってきたが、もう一つのrとθの極座標系でも表すことができる・・・という話に進むのだろうか。 「三角法」の入門I、ということで、ここはサッサと進めていこう。

三角法の定義は以下で全てである。角度θ(シータ)に対する三角関数、つまりサイン・コサイン・タンジェントの定義も以下の通りである。

英語で「soh-cah-toa」と言う、というのは初めて知ったが、　これは以下のように定義されている。 日本語の場合も、三角形の2辺を「s」「c」「t」の筆記体の筆順の一部でなぞって覚えたが、同じようなものだろう。

• soh stands for "sine equals opposite over hypotenuse." "Opposite" refers to the side opposite the angle.
• cah stands for "cosine equals adjacent over hypotenuse." "Adjacent" is the side next to the angle.
• toa refers to "tangent equals opposite over adjacent."

ここまでは第1象限、つまりθの角度の頂点を原点としてθが0度から90度までの範囲だが、正の値の辺を持つ三角形を離れて、θをぐるりと一周する「三角関数」に概念を拡大すると、以下のように、「辺」という概念は正負の領域に広がった変数となる。 ここでは、三角比は「比」なので、円の半径に依存しないことから、「単位円(unit circle)」として半径1の円を考える。 また、角度θも「度」から「ラジアン(radian)」に拡張される。180度がπラジアンである。

なお、円周率「π」については、昔のPowerBook520cで計算した 10万桁のπ とか、昔のG3PowerBookで計算した 100万桁のπ とか、 実験でπを求める というのもあるので参照されたい(^_^;)。

上の単位円のある座標系で、中心角がθである点Pの座標は、半径rと中心角θによる極座標(r, θ)で表されるが、これを2次元直交座標系と見れば、点Pの座標(x, y)は、三角関数を使って以下のように表せる。

x = cosine(theta) * radius
y = sine(theta) * radius

上の書き方は一般的な数学での表記であり、Processingでは以下のように表現する。

float x = cos(radians(angle)) * radius;
float y = sin(radians(angle)) * radius;

角度については、thetaと書いたらラジアン単位、angleと書いたら「度」なので、これらの相互変換は以下の計算で行える。 piはもちろん円周率である。

theta = angle*pi/180
angle = theta*180/pi

この変換のために、Processingでは以下の関数「radians」「degrees」が提供されている。

theta = radians(angle)
angle = degrees(theta)

単位円での定義から、三角関数は円周上の点の回転移動そのものに関係していることは明白だが、これをアニメーションで示したProcessingのサンプルがあった。 アプレットとして書き出してみると、このようになった。

float px, py, px2, py2;
float angle, angle2;
float radius = 100;
float frequency = 2;
float frequency2 = 2;
float x, x2;

PFont myFont;

void setup(){
	size(600, 200);
	background (127);
	myFont = createFont("verdana", 12);
	textFont(myFont);
}

void draw(){
	background (127);
	noStroke();
	fill(255);
	ellipse(width/8, 75, radius, radius);
	px = width/8 + cos(radians(angle))*(radius/2);
	py = 75 + sin(radians(angle))*(radius/2);
	rectMode(CENTER);
	fill(0);
	rect (px, py, 5, 5);
	stroke(100);
	line(width/8, 75, px, py);
	stroke(200);
 	angle2 = 0;

	for (int i = 0; i< width; i++)
		{
			px2 = width/8 + cos(radians(angle2))*(radius/2);
			py2 = 75 + sin(radians(angle2))*(radius/2);
			point(width/8+radius/2+i, py2);
			angle2 -= frequency2;
		}
	noStroke();
	ellipse(width/8+radius/2+x, py, 5, 5);
	angle -= frequency;
	x+=1;
	if (x>= width-60) 
		{
			x = 0;
			angle = 0;
		}
	stroke(50);
	line(px, py, width/8+radius/2+x, py);
	text("y = sin x", 35, 185);
	text("px = " + px, 105, 185);
	text("py = " + py, 215, 185);
}

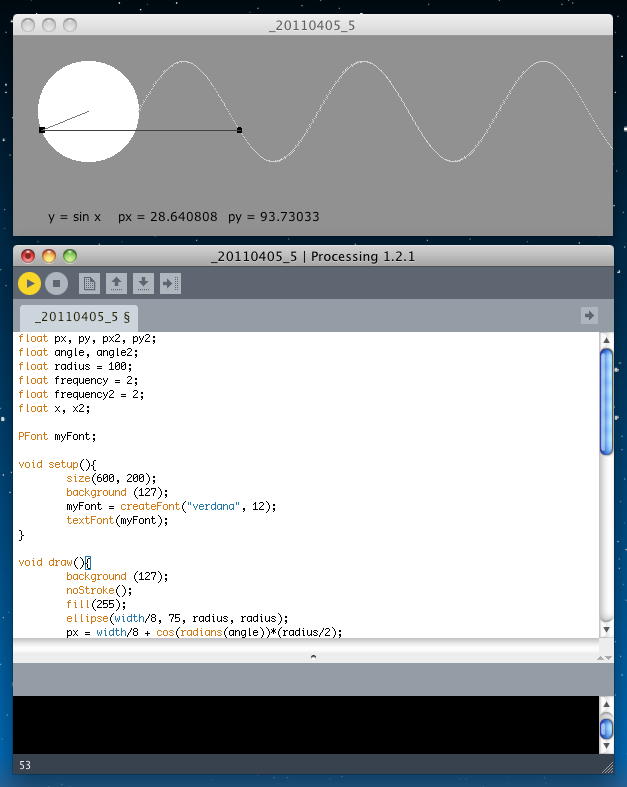
この動きは、ちょうど2回生向けに始めた「サウンドデザイン」で紹介した話そのもので、とても判りやすい。 さっそく、このリンクを講義用教材ページに設定した。 これでこのセクションはおしまいである。 まぁ、定義だけなので「入門編」なのだろう(^_^;)。 次は チュートリアル の PVector である。 三角関数に続いて「ベクトル」かな。 なんか、高校の数学の復習をしているみたいである。 ベクトルの定義は以下のように明快である。

ここでまず、Processingのビギナーがここまでに作ったであろう「跳ねる玉」プログラムの復習が登場する。 これは「Example: Bouncing Ball with No Vectors」ということで、ベクトルの概念ナシに、壁で完全弾性衝突し続けるボールの運動を描画する。 ここには物理的なベクトルの概念は無くて、単に数学的に、境界に来たら進行方向の座標の向きを切り替える、というだけの等速直線運動として記述している。 以下のサンプルであり、 アプレットとして書き出してみると、このようになった。

float x = 100;
float y = 100;
float xspeed = 1;
float yspeed = 3.3;

void setup() {
	size(200,200);
	smooth();
	background(255);
}

void draw() {
	noStroke();
	fill(255,10);
	rect(0,0,width,height);
	x = x + xspeed;
	y = y + yspeed;
	if ((x > width) || (x < 0)) 
		{
			xspeed = xspeed * -1;
		}
	if ((y > height) || (y < 0)) 
		{
			yspeed = yspeed * -1;
		}
	stroke(0);
	fill(175);
	ellipse(x,y,16,16);
}

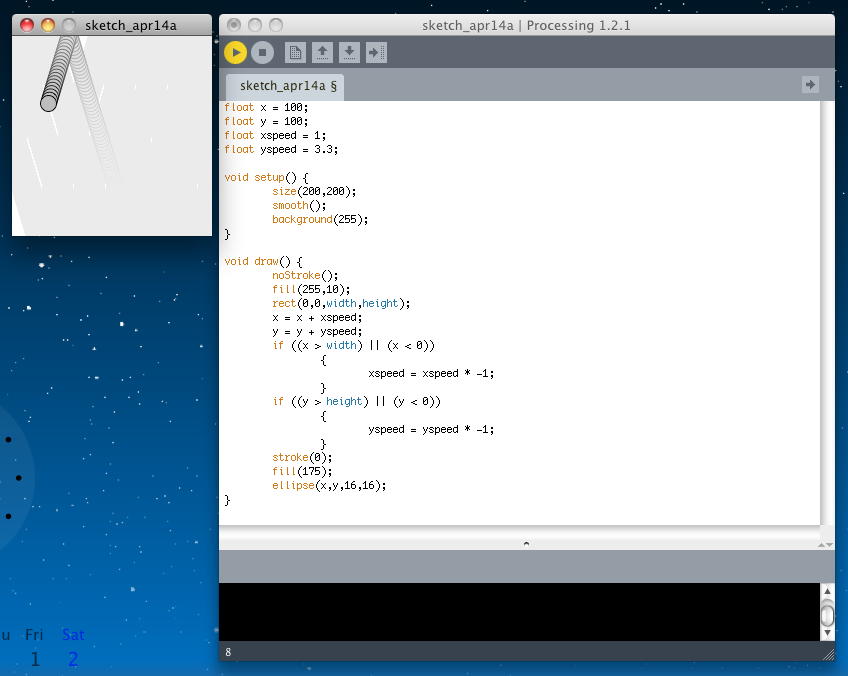
このアプレットは、僕が1995年ごろ、初めてJavaを勉強し始めて3日目に作った、以下のJavaアプレットと同じ原理で動いている。ナツカシス(^_^)。

source

ところで、 このアプレット でバウンドしているボールには、以下のようなプロバティがある。

• LOCATION: x and y
• SPEED: xspeed and yspeed

もう少し高度なProcessingスケッチを考えると、さらにこのボールに以下のようなプロパティを与えることが考えられる。

• ACCELERATION: xacceleration and yacceleration
• TARGET LOCATION: xtarget and ytarget
• WIND: xwind and ywind
• FRICTION: xfriction and yfriction

ACCELERATIONとは加速度である。上の例では宇宙空間(地球上を周回する人工衛星の機内とか宇宙空間を推力ナシで移動する宇宙船の機内と同様の、摩擦のない等速直線運動)みたいであるが、実際には、摩擦による加速度(減速)とか、地球上の引力(重力)による加速度などが考えられる。
TARGET LOCATIONとは、領域の境界の壁まで行って衝突するのでなく、ぶつかるターゲットの座標である。
WINDとは、ゲームなどでよくある、一定方向の風に流されるようなファクターである。 このFlashでも使われている。
FRICTIONとは摩擦である。動摩擦係数であれば一定の力なのでマイナスの加速度に直結するが、静摩擦係数となると不連続特性なので厄介である。

このような複雑なファクターが加わった場合、「float x;」「float y;」「float xspeed;」「float yspeed;」というような変数による単純なモデルではその物理的現象を記述できないので、以下のようにベクトル変数を用いることになる。 これがこのセクションの主題である。

Vector location;
Vector speed;

技術的には、ベクトルとは以下のように、「2点間の座標の差分」である。 ある場所から他の場所に行く時に、「北に何歩」「東に何歩」と指定するのと同じである。 京都市内で言えば「百万遍から東大路通を北に50m、今出川通を東に200mの場所」が京大理学部である、というようなものである。

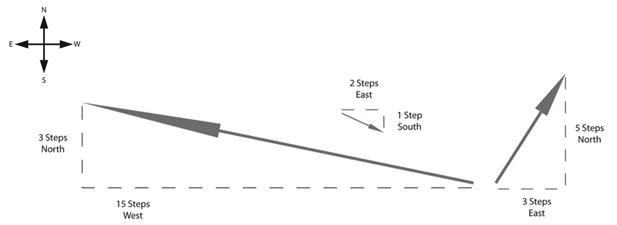
上の意味は以下である。

• ( 3, 5)　→　Walk three steps east, turn and walk five steps north.
• ( 2,-1)　→　Walk two steps east, turn and walk one step south.
• (-15, 3)　→　Walk fifteen steps west, turn and walk three steps north.

Processingのプログラマにとってベクトルとは、以下のように、ある点の場所(location)から、別の点の場所(location)に移動させるものとして「pixel velocity」と呼ぶらしい。

ベクトルとはある方向にある大きさだけ移動させる、という量でしかないので、これだけでは特定の点の場所(location)は規定できない。 起点の場所とベクトルがあれば、終点の場所が確定する。 そこで、さきの「バウンドするボール」のサンプルを、以下のように対応させて改めて記述することを考えよう。

• location　→　x,y
• velocity　→　xspeed,yspeed

このようなベクトルは、以下のようなクラスで定義する。ここでは2つの引数であるが、3つにすれば3次元ベクトルも扱える。 無限次元ベクトルには拡張できないので、宇宙物理学/素粒子物理学のシミュレーションはちょっと難しいかもしれない(^_^;)。

class PVector{
	float x;
	float y;
	PVector(float x_, float y_) 
		{
			x = x_;
			y = y_;
		}
}

これを使うと、ここまでは

float x = 100;
float y = 100;
float xspeed = 1;
float yspeed = 3.3;

などとしていた定義が、以下のようになる。

PVector location = new PVector(100,100);
PVector velocity = new PVector(1,3.3);

つまり、ここまでは

// Add the current speed to the location.
x = x + xspeed;
y = y + yspeed;

などとしていた処理を、ベクトルでまとめて以下のように記述する。★なお、これは暫定的な表示である。

// Add the current velocity vector to the location vector.
location = location + velocity;

ここまでの準備を経て、次のトピックは「ベクトルの加算」である。 ベクトルはたまたま並行である場合以外は方向がばらばらなので、その加算は独立な座標成分ごとに、という事である。 言い方を帰ると、あるベクトルの終点に加算するベクトルの起点を移動させると、この2つのベクトルを加算したベクトルの起点は最初のベクトルの起点、この2つのベクトルを加算したベクトルの終点は、以下のように連結された第二のベクトルの終点となる。

これを「PVector」クラスの中に「add()」という関数として定義すると、以下のようになる。

class PVector {
	float x;
	float y;
	PVector(float x_, float y_) 
		{
			x = x_;
			y = y_;
		}
	// New!  A function to add another PVector to this PVector.  
	// Simply add the x components and the y components together.
	void add(PVector v) 
		{
			x = x + v.x;
			y = y + v.y;
		}
}

これにより、さきに★暫定的に書いていた「location = location + velocity;」は、「location.add(velocity);」と美しく記述できる。 ここまでをまとめると、さきの「バウンドするボール」のProcessingプログラムは、以下のようになる。 アプレットとして書き出してみると、このようになった。

PVector location;
PVector velocity;

void setup() {
	size(200,200);
	smooth();
	background(255);
	location = new PVector(100,100);
	velocity = new PVector(2.5,5);
}

void draw() {
	noStroke();
	fill(255,10);
	rect(0,0,width,height);
	location.add(velocity);
	if ((location.x > width) || (location.x < 0)) 
		{
			velocity.x = velocity.x * -1;
		}
	if ((location.y > height) || (location.y < 0)) 
		{
			velocity.y = velocity.y * -1;
		}
	stroke(0);
	fill(175);
	ellipse(location.x,location.y,16,16);
}

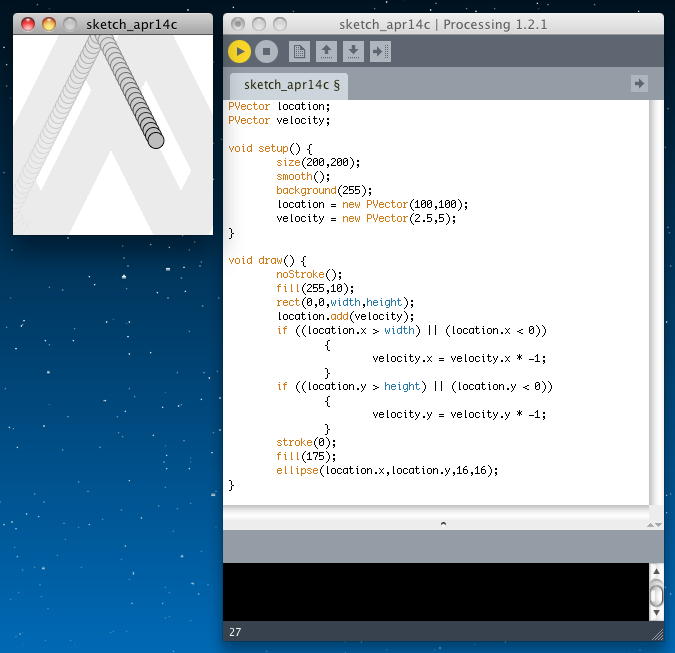
この例では出力の描画は変わっていないし、あまり大きな違いがないように思えるかもしれないが、実は大きな進歩がある。 例えば最終的に円を描画する「ellipse(location.x,location.y,16,16);」から判ることとして、関数「ellipse()」は引数として座標の数値を受け取るために、ベクトルの「location」でなく、ドットで切った「location.x」というプロパティの数値を渡しているのである。

すでにベクトルの加算として「add()」を見てきたが、ベクトルには以下のような、たくさんの演算関数が用意されている。 以下、もっとも基本的な6つを順に解説していく。

• add() -- add vectors
• sub() -- subtract vectors
• mult() -- scale the vector with multiplication
• div() -- scale the vector with division
• mag() -- calculate the magnitude of a vector
• normalize() -- normalize the vector to unit length of 1
• limit() -- limit the magnitude of a vector
• heading2D() -- the heading of a vector expressed as an angle
• dist() -- the euclidean distance between two vectors (considered as points)
• angleBetween() -- find the angle between two vectors
• dot() -- the dot product of two vectors
• cross() -- the cross product of two vectors

まず、ベクトルの減算「sub()」は以下のように、加算の逆演算として考えることが出来る。 ベクトルの座標には正負があるので、ベクトルでは「負の長さ」のように考えてもいいので、実数の範囲ではベクトルの加算と減算は同じことである。

具体的な「sub()」の活用例として、マウスのカーソルを追いかけて直線を描画するProcessingプログラムは以下のようになる。 これは常に、マウスの座標と画面中心座標のそれぞれのベクトルの差をとっている。 アプレットとして書き出してみると、このようになった。

void setup() {
	size(200,200);
	smooth();
}

void draw() {
	background(255);
	PVector mouse = new PVector(mouseX,mouseY);
	PVector center = new PVector(width/2,height/2);
	mouse.sub(center);
	translate(width/2,height/2);
	line(0,0,mouse.x,mouse.y);
}

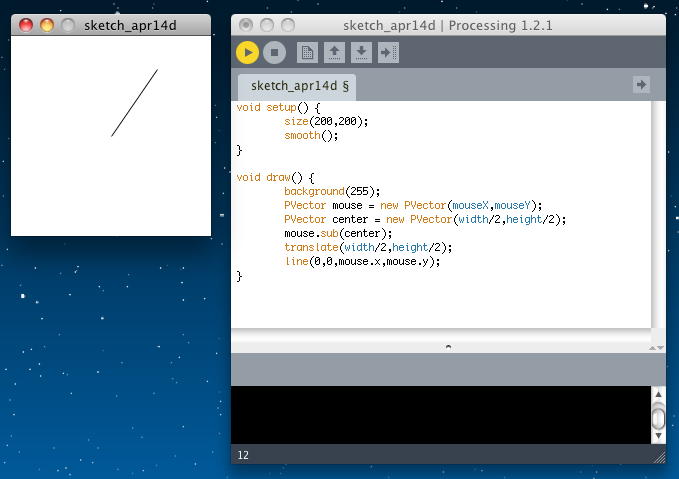
次に、ベクトルには、実数倍(スカラー倍)という演算がある。「mult()」である。 ベクトルのそれぞれの成分に、尾などスカラーを乗算する、というものである。 これは以下のように「実数×ベクトル」という演算である。

void mult(float n) {
	x = x * n;
	y = y * n;
}

具体的な「mult()」の活用例として、さきのマウスのカーソルを追いかけて直線を描画するProcessingプログラムを以下のようにすると、 画面中央からマウスポインタに向かうベクトルの途中までの描画が追いかけてくる。 アプレットとして書き出してみると、このようになった。

void setup() {
	size(200,200);
	smooth();
}

void draw() {
	background(255);
	PVector mouse = new PVector(mouseX,mouseY);
	PVector center = new PVector(width/2,height/2);
	mouse.sub(center);
	mouse.mult(0.5);
	translate(width/2,height/2);
	line(0,0,mouse.x,mouse.y);  
}

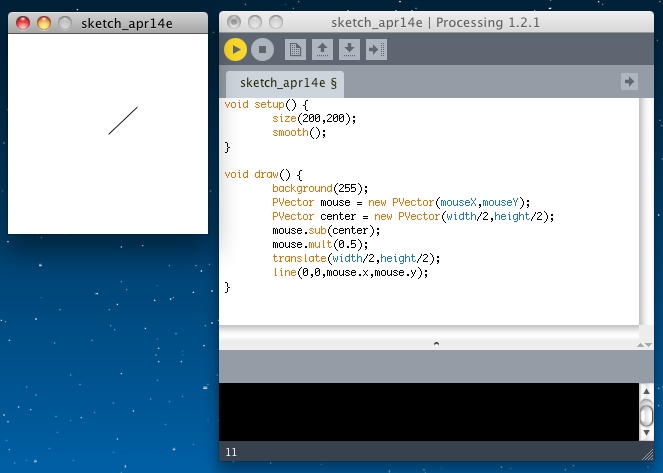
ベクトルをスカラー乗算する「mult()」と同様に、ベクトルをスカラー除算する以下の「div()」がある。 これも、ゼロでの除算を禁止して除いている以外は同様に、実数であれば拡大縮小は同じことになる。

void div(float n) {
	x = x / n;
	y = y / n;
}

次に、ベクトルの大きさを与える「mag()」である。 これは以下のように、ピタゴラスの定理から、x方向、y方向それぞれの成分の2乗和の平方根である。 ベクトルvの大きさを　| | v | | 　とも書く。

float mag() {
	return sqrt(x*x + y*y);
}

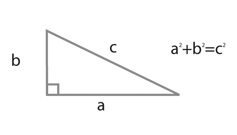
具体的な「mag()」の活用例として、さきのマウスのカーソルを追いかけて直線を描画するProcessingプログラムを以下のようにすると、 画面中央からマウスポインタへのベクトルの大きさが棒グラフで表示される。 アプレットとして書き出してみると、このようになった。

void setup() {
	size(200,200);
	smooth();
}

void draw() {
	background(255);
	PVector mouse = new PVector(mouseX,mouseY);
	PVector center = new PVector(width/2,height/2);
	mouse.sub(center);
	float m = mouse.mag();
	fill(0);
	rect(0,0,m,10);  
	translate(width/2,height/2);
	line(0,0,mouse.x,mouse.y);
}

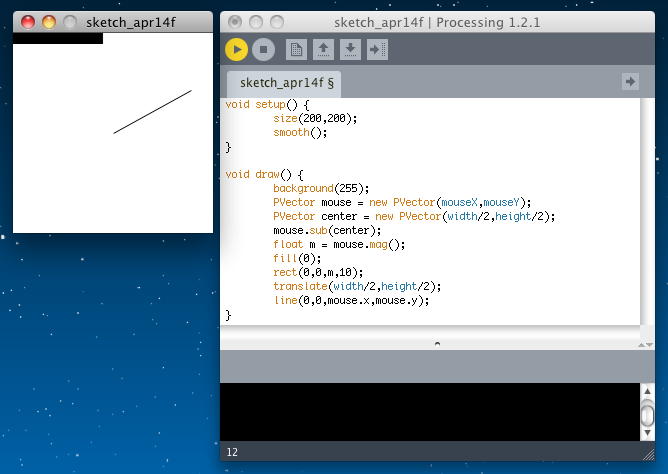
ベクトルに対する次の関数は「normalize()」である。これはベクトルの方向を変えずに、その長さを「単位ベクトル」、つまり長さ=1に変換する。 演算としては以下のように、ベクトルの各成分を、そのベクトルの大きさで割ればよい。 当然ながら、ゼロベクトルには定義されない。

void normalize() {
	float m = mag();
	if (m != 0) 
		{
			div(m);
		}
}

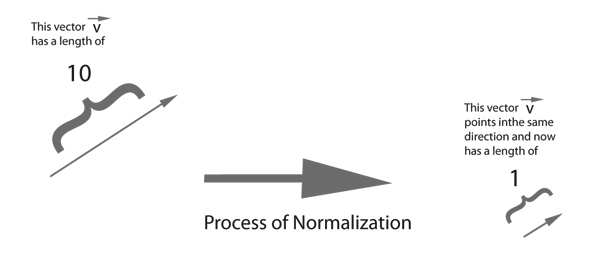
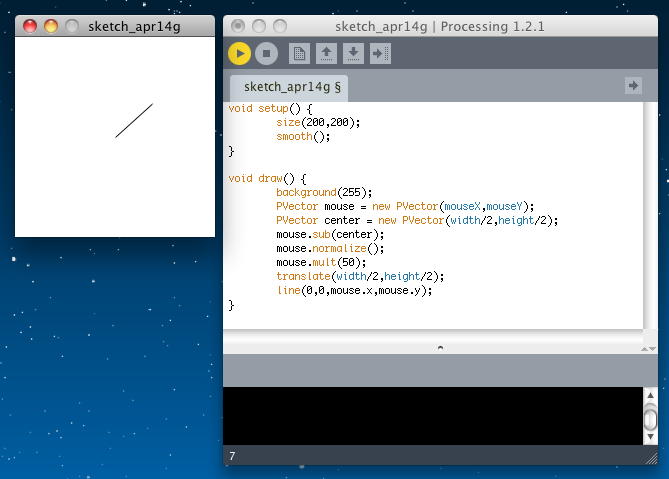
具体的な「normalize()」の活用例として、さきのマウスのカーソルを追いかけて直線を描画するProcessingプログラムを以下のようにすると、 画面中央からマウスポインタへのベクトルをノーマライズした単位ベクトルが表示される。 アプレットとして書き出してみると、このようになった。

void setup() {
	size(200,200);
	smooth();
}

void draw() {
	background(255);
	PVector mouse = new PVector(mouseX,mouseY);
	PVector center = new PVector(width/2,height/2);
	mouse.sub(center);
	mouse.normalize();
	mouse.mult(50);
	translate(width/2,height/2);
	line(0,0,mouse.x,mouse.y);  
}

まだ解説していないベクトルの演算があるが、ここで話は「Vectors: Motion」ということで、動きにベクトルを使うことの意味に移っている。 Processingはオブジェクト指向なので、オブジェクト指向の発想から、ProcessingでMotionを面白く発展させようというのである。 以下の例では、動くもの「mover」というオブジェクト自体のコンストラクタの中に、自分の移動ベクトル(velocity)をランダムウォークで生成するルールを記述することで、「自分で行き先を作りながら描画するやつ」というボールが動き回るプログラムを実現している。 アプレットとして書き出してみると、このようになった。

Mover mover;

void setup() {
	size(200,200);
	smooth();
	background(255);
	mover = new Mover(); 
}

void draw() {
	noStroke();
	fill(255,10);
	rect(0,0,width,height);
	mover.update();
	mover.checkEdges();
	mover.display(); 
}

class Mover {
	PVector location;
	PVector velocity;

	Mover() {
		location = new PVector(width/2, height/2);
		velocity = new PVector(0, 0);
	}

	void update() {
		velocity = new PVector(random(-2,3),random(-2,3));
		location.add(velocity);
	}

	void display() {
		stroke(0);
		fill(175);
		ellipse(location.x,location.y,16,16);
	}

	void checkEdges() {
		if (location.x > width) {
			location.x = 0;
		} else if (location.x < 0) {
			location.x = width;
		}   
		if (location.y > height) {
			location.y = 0;
		} else if (location.y < 0) {
			location.y = height;
		}
	}
}

物理学では加速度accelerationのことを「速度の時間的変化」と定義するが、Processingにおいては、オブジェクトのMotionのvelocityを変化させるもの、というより広い定義で、以下のような色々な加速度accelerationのアルゴリズムを提供している。 これを用いると、数学に深入りすることなく、インタラクティブなインスタレーションのようなものを簡単に作ることが出来てしまう。

• Make up a constant acceleration
• A totally random acceleration
• Perlin noise acceleration
• Acceleration towards the mouse

もうじきこのsectionの最後のサンプル(Acceleration towards the mouse)になるのだが、その前に「Vectors: Static vs. Non-Static」という解説が立ちはだかる。 vectorsクラスやPVector classを使う上で、「static methods」と「non-static methods」とがあるのだという。 以下、ちょっとこれまでのベクトルを忘れて考えていく。

float x = 0;
float y = 5;

x = x + y;

まず、上のコードは簡単である。xの初期値は0、ここに初期値5であるyを加算したものがxになるので、最後の段階でx = 5である。 これを、既に学んだPVectorでもやってみよう。

PVector v = new PVector(0,0);
PVector u = new PVector(4,5);

v.add(u);

上のコードでは、ベクトルvの初期値は(0, 0)で、ここに初期値(4, 5)であるベクトルuを「add()」で加算する。 その結果、最後の段階ではvは(4, 5)である。 ここまでは問題ない。

float x = 0;
float y = 5;

float z = x + y;

上のコードでは、xの初期値は0、yの初期値は5、そしてこれらの加算結果を新しく定義した変数zに格納しているので、xもyも変化していない。 これもOKである。 ただし、これを形式的にPVectorに真似た以下の例は間違いである。

PVector v = new PVector(0,0);
PVector u = new PVector(4,5);

PVector w = v.add(u); // Don't be fooled, this is incorrect!!!

上の記述が間違いなのを確認するために、以下の「add()」の定義を思い出そう。 「add()」は(リターンの)型がvoidなのでベクトルを返さないし、この定義からベクトルx自身の要素が変わってしまうので、これは間違いなのである。

void add(PVector v) {
	x = x + v.x;
	y = y + v.y;
}

2つのPVectorオブジェクトを加算して、結果として新しいPVectorオブジェクトを返すためには、我々はstaticなadd()関数を使わなければならない。 staticな関数とは以下のように、クラス名自身で呼ばれる関数のことで、オブジェクトのインスタンスではないのだという。

// Assuming two PVector objects: v and u

// Static: called off of the class name.
PVector.add(v,u);

// Not static: called off of an object instance.
v.add(u);

ベクトルの場合には明示的にstaticとしないといけない、として以下の例が書かれているが、これは謎である。 xとyが何なのか、まったく書かれていない(^_^;)。

static PVector add(PVector v1, PVector v2) {
	PVector v3 = new PVector(v1.x + v2.x, v1.y + v2.y);
	return v3;
}

これはベクトルの内積でもないし、一体何なのか不明であるが、とりあえず解説としては以下のように続いている。

• The function is labeled as static.
• The function does not have a void return type, but rather returns a PVector.
• The function creates a new PVector (v3) and returns the result of adding the components of v1 and v2 in that new PVector.

それは判ったが、上のxとyは何なのか、答えてくれていない(^_^;)。 以下のようにすれば正しいのだよ、とあるが、うーーーーむ、これでは具体的にwが判らないんですけど。(^_^;)

PVector v = new PVector(0,0);
PVector u = new PVector(4,5);
// The static version of add allows us to add two PVectors 
// together and assign the result to a new PVector while 
// leaving the original PVectors (v and u) intact.
PVector w = PVector.add(v,u);

なんか騙されたようなカンジのまま、ここで最後の「Vectors: Interactivity」となった。 ここでは、マウスのカーソル位置をベクトルの片方と設定して、以下のようにインタラクティブに動くもの、というような動作をさせるらしい。

およそ、ここまでに登場したものを組み合わせて、なかなか面白い以下のようなプログラムである。 アプレットとして書き出してみると、このようになった。

Mover[] movers = new Mover[20];

void setup() {
	size(200,200);
	smooth();
	background(255);
	for (int i = 0; i < movers.length; i++) {
		movers[i] = new Mover(); 
	}
}

void draw() {
	noStroke();
	fill(255,10);
	rect(0,0,width,height);
	for (int i = 0; i < movers.length; i++) {
		movers[i].update();
		movers[i].checkEdges();
		movers[i].display(); 
	}
}

class Mover {
	PVector location;
	PVector velocity;
	PVector acceleration;
	float topspeed;

	Mover() {
		location = new PVector(random(width),random(height));
		velocity = new PVector(0,0);
		topspeed = 4;
	}

	void update() {
		PVector mouse = new PVector(mouseX,mouseY);
		PVector dir = PVector.sub(mouse,location);
		dir.normalize();     // Normalize
		dir.mult(0.5);       // Scale 
		acceleration = dir;  // Set to acceleration
		velocity.add(acceleration);
		velocity.limit(topspeed);
		location.add(velocity);
	}

	void display() {
		stroke(0);
		fill(175);
		ellipse(location.x,location.y,16,16);
	}

	void checkEdges() {
		if (location.x > width) {
 			location.x = 0;
		} else if (location.x < 0) {
			location.x = width;
		}
		if (location.y > height) {
			location.y = 0;
		}  else if (location.y < 0) {
			location.y = height;
		}
	}
}

staticの謎は残ったままだが、これでこのセクションは終わりである。 次回は チュートリアル の Anatomy of a Program からという事になる。

2011年5月10日(火)

前回の日記が4月14日で、約1ヶ月も空いてしまった。 この間、 将棋 とか 新歓 とか 34虎 とか 誕生日 とかいろいろあって、もうほとんど忘却の彼方であるが、「音楽情報科学」の講義の中でProcessingを紹介したので、 なんとしても進展していかなければならなくなった(^_^;)。 SuperCollider日記 の方も相当に空いてしまっているが、まずはProcessingからである。

前回の続きとして、今日は チュートリアル の Anatomy of a Program からである。 ここまではProcessingプログラミングのいろいろな要素を見て来たが、ここでは「プログラムの構造/構想/構成」ということで、 漠然としたアイデアをいかにProcessingで具現化するか、というプロセスを解説する模様である。 具体的な目標として「正多角形を描画する」というテーマを掲げた。

最初の第1ステップは「紙の上でプランを立てる」という事である。 以下のように、半径rの円に内接する正多角形の場合、その円の中心と各頂点を結ぶ線分のなす中心角は、「360度を頂点数で割った角度」というものになる。 これを使うためには、半径と中心角θとを使った三角法が必須となる。

そこで次の第2ステップとして、基礎的な三角法として、以下のような関係を確認する。 Processingでは、x方向は一般の座標軸と同じだが、y方向はコンピュータスクリーンの作法に合わせているので、通常の数学の三角関数とはθの方向が逆になっている。 θは右回り(時計方向の回転)が正であり、y軸は「下が正」ということである。

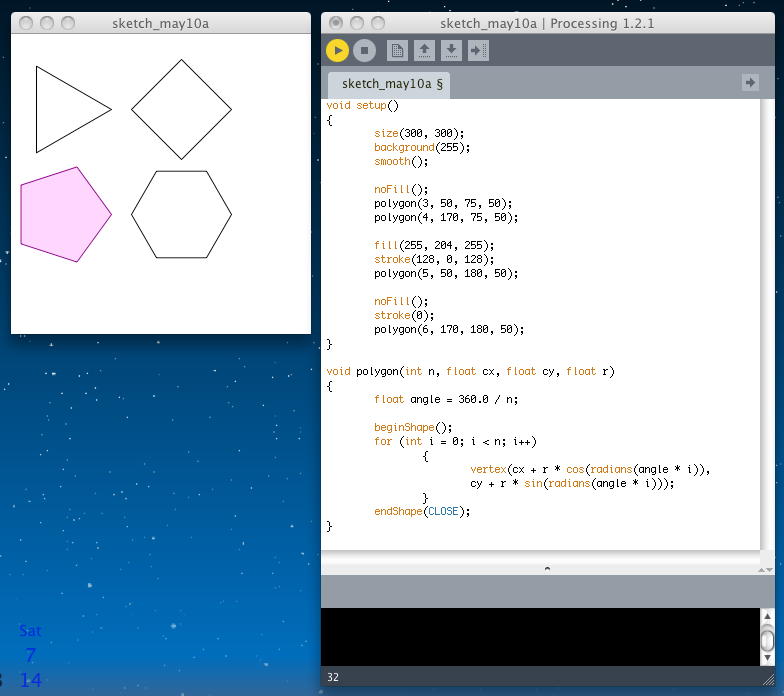
第3ステップは「デザインの決定」である。 以下のプログラムのように、定義さえしっかりすれば、正三角形、正方形、正5角形、正6角形、は簡単にプログラムできる。 ここでのポイントは、「正○角形を描く」という関数「polygon(int n, float cx, float cy, float r)」を定義しているところである。 第1の引数は「正○角形」という○の部分、第2と第3の引数は正多角形の内接円の中心座標、第4の引数はその半径である。

void setup()
{
	size(300, 300);
	background(255);
	smooth();

	noFill();
	polygon(3, 50, 75, 50);
	polygon(4, 170, 75, 50);

	fill(255, 204, 255);
	stroke(128, 0, 128);
	polygon(5, 50, 180, 50);

	noFill();
	stroke(0);
	polygon(6, 170, 180, 50);
}

void polygon(int n, float cx, float cy, float r)
{
	float angle = 360.0 / n;

	beginShape();
	for (int i = 0; i < n; i++)
		{
			vertex(cx + r * cos(radians(angle * i)),
			cy + r * sin(radians(angle * i)));
		}
	endShape(CLOSE);
}

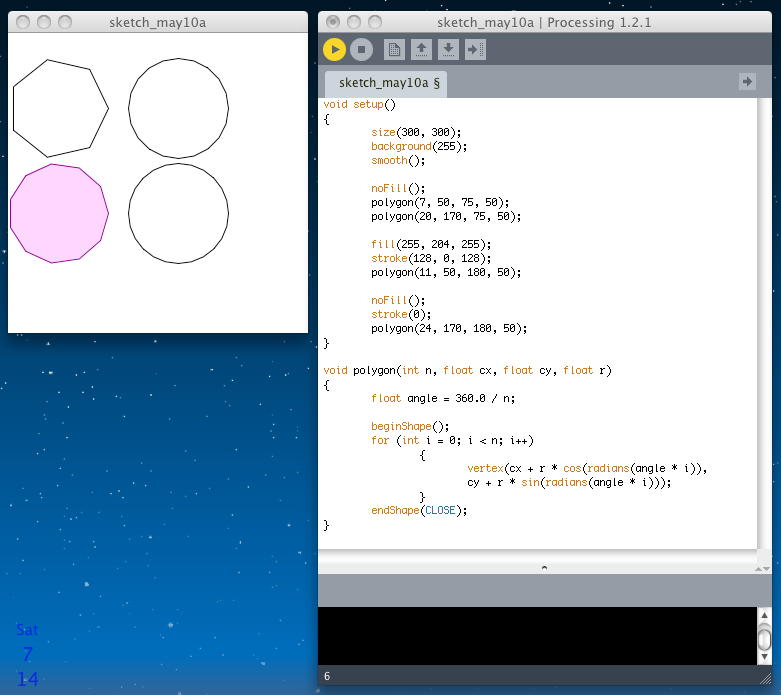
この「正○角形を描く」という関数「polygon(int n, float cx, float cy, float r)」は汎用なので、 単純に○の数字を変えるだけで、以下のように正7角形でも正11角形でも正20角形でも正24角形でもいくらでも出来る。

void setup()
{
	size(300, 300);
	background(255);
	smooth();

	noFill();
	polygon(7, 50, 75, 50);
	polygon(20, 170, 75, 50);

	fill(255, 204, 255);
	stroke(128, 0, 128);
	polygon(11, 50, 180, 50);

	noFill();
	stroke(0);
	polygon(24, 170, 180, 50);
}

void polygon(int n, float cx, float cy, float r)
{
	float angle = 360.0 / n;

	beginShape();
	for (int i = 0; i < n; i++)
		{
			vertex(cx + r * cos(radians(angle * i)),
			cy + r * sin(radians(angle * i)));
		}
	endShape(CLOSE);
}

次のトピックは「2歩進んで1歩戻る」とある。 とりあえずプログラムが出来たとしても、そこから改良していくことが重要なのである。

まず、上の正多角形の例は、よく見ると、なんだか美しくない(^_^;)。 これは例えば正三角形や正5角形が、「底辺が水平で座りがいい」状態になっていない、あるいは左右対称でないからである。 もともと上の定義では、基準点(内接円の中心)から右方向に伸ばした水平線があり、この上に最初の頂点がある。 そこから時計方向に中心角θだけ回転させて次の頂点を決めているので、どうやっても座りが悪いのである。 これは実は、図形全体を回転させる「rotate()」関数で解決する。 ただし次の改良例では、最初の角度基準の頂点を、水平方向に対してどれだけの角度とするか、というパラメータとして、さらに引数を追加することにしている。 また、角度を「度」でなくラジアン指定できるようにしている。

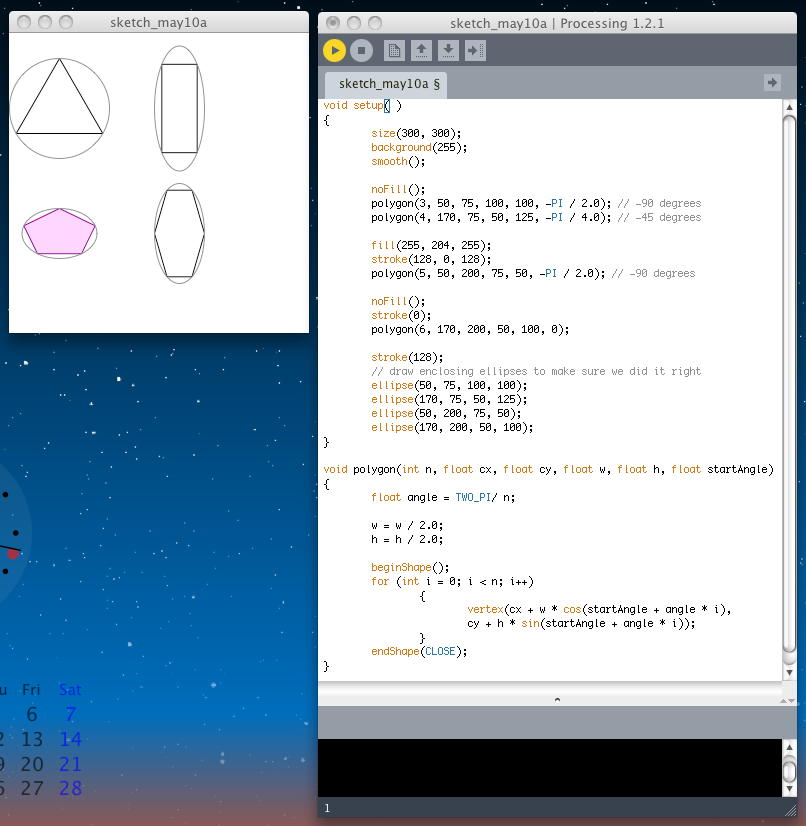
また、内接するのが円だけではなくて、楕円に変形したところに内接させたくなる。 これは正○角形ではなくなるが、アンパンマンでも瓜実顔でも描くためには、widthとheightとで内接円を楕円に変形するためのパラメータとして、さらに引数を追加したくなる。 これらをまとめて改良したのが、以下の例である。 図形の座りも良くなり、プロポーションの変形も可能となった。(^_^)

void setup( )
{
	size(300, 300);
	background(255);
	smooth();

	noFill();
	polygon(3, 50, 75, 100, 100, -PI / 2.0); // -90 degrees
	polygon(4, 170, 75, 50, 125, -PI / 4.0); // -45 degrees

	fill(255, 204, 255);
	stroke(128, 0, 128);
	polygon(5, 50, 200, 75, 50, -PI / 2.0); // -90 degrees

	noFill();
	stroke(0);
	polygon(6, 170, 200, 50, 100, 0);

	stroke(128);
	// draw enclosing ellipses to make sure we did it right
	ellipse(50, 75, 100, 100);
	ellipse(170, 75, 50, 125);
	ellipse(50, 200, 75, 50);
	ellipse(170, 200, 50, 100);
}

void polygon(int n, float cx, float cy, float w, float h, float startAngle)
{
	float angle = TWO_PI/ n;

	w = w / 2.0;
	h = h / 2.0;

	beginShape();
	for (int i = 0; i < n; i++)
		{
			vertex(cx + w * cos(startAngle + angle * i),
			cy + h * sin(startAngle + angle * i));
		}
	endShape(CLOSE);
}

次のトピックは「パラメータが多過ぎる」(^_^;)である。 上の例では、いろいろやりたい事に対応するために、パラメータとして多くの引き数を持つ関数「polygon(int n, float cx, float cy, float w, float h, float startAngle)」を作っておいて、勝手な話である。 ここでは、たいていの場合には「正○角形」である、つまり、widthとheightとで内接円を楕円に変形することはない、というようにしたい。 そこで使えるテクニックが「overload」というものである。 これは、上記のサンプルにあった、あらかじめ全てのパラメータの定義とともにある「polygon(int n, float cx, float cy, float w, float h, float startAngle)」の定義にさらに加えて、

void polygon(int n, float cx, float cy, float r)
{
	polygon(n, cx, cy, r * 2.0, r * 2.0, 0.0);
}

という記述を定義することで実現できる。 これにより、最初の定義で6個あった引き数に対して、新たに定義された「polygon(int n, float cx, float cy, float r)」では、内部的に対応した計算を行った、4つの引き数のシンブルな関数として呼び出すことができる。 これにより、以下のようにシンプルに記述が出来る、ということである。

void setup()
{
	size(300, 300);
	background(255);
	smooth();
  
	noFill();
	polygon(3, 70, 75, 50); // use the defaults
	polygon(4, 170, 75, 25);
  
	stroke(128);
	// draw enclosing ellipses to make sure we did it right
	ellipse(70, 75, 100, 100);
	ellipse(170, 75, 50, 50);
}

void polygon(int n, float cx, float cy, float w, float h, float startAngle)
{
	float angle = TWO_PI/ n;

	w = w / 2.0;
	h = h / 2.0;

	beginShape();
	for (int i = 0; i < n; i++)
		{
			vertex(cx + w * cos(startAngle + angle * i),
			cy + h * sin(startAngle + angle * i));
		}
	endShape(CLOSE);
}

void polygon(int n, float cx, float cy, float r)
{
	polygon(n, cx, cy, r * 2.0, r * 2.0, 0.0);
}

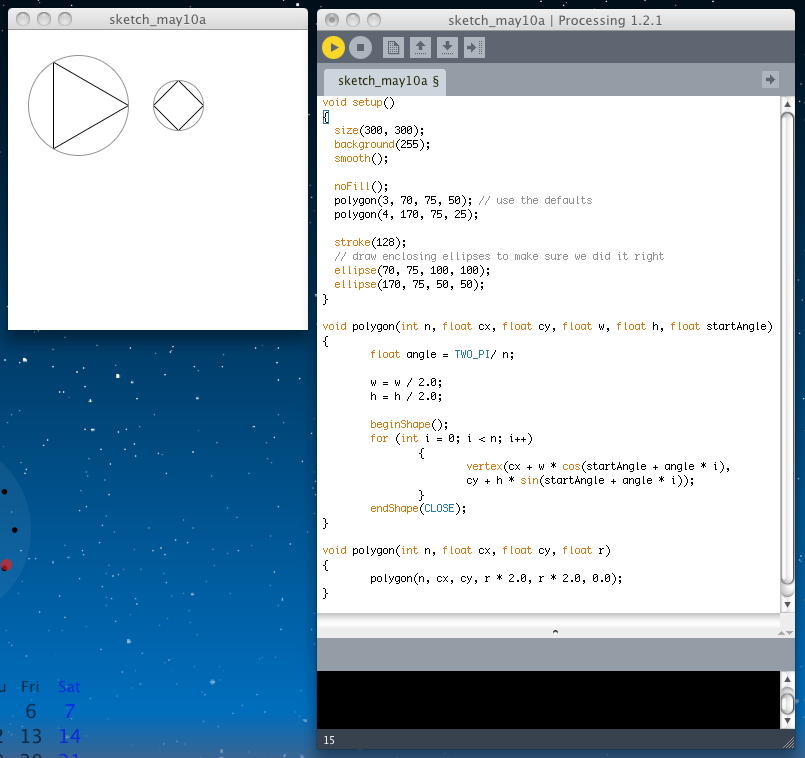
次のトピックは「Safe Computing」である。 これは初心者には気付きにくいが、馴れた者なら無意識にやっている事である。 上の例で、「正○角形」の中心角を計算するところで、「2πを引き数nで割る」となにげに記述していた。 しかしこれはコンピュータにとっては恐怖の演算である。 多くの場合、数値の初期値はゼロであり、もしn=0で呼び出されれば、数学では禁忌とされている「ゼロでの除算」という事になる。 昔のコンピュータの場合、この瞬間にパソコンがフリーズして、ソフトリセットすら受け付けない事も多かった。 そうなると電源を強制断するだけしかない。 この場合、作りかけたプログラムが保存されていなかったり・・・と良くない事が続く。(^_^;)

そこで「Safe Computing」である。 万一、n=0で呼び出されてもトラブルが無いように、以下のようにしましょうね、という事である。

void polygon(int n, float cx, float cy, float w, float h, float startAngle)
{
	f (n > 2)
		{
			float angle = TWO_PI/ n;
			.
			 .
			beginShape()
			.
			.
			endShape(CLOSE);
		}
}

まぁ、こんなところにいちいち構っていては楽しいプログラミングが楽しくなくなるので、 何か起きた時にそこで考える(デバッグ)、というのもアリである。(^_^;)

さて、次のテーマは「星形を描く」である。 これは以下のようなアイデアスケッチからスタートする。 描いてみれば、何をすればいいのか、判ってくるものである。

基本的には「正○角形」の描画と似ていて、中心角の半分のところで、半径方向に一定の割合で「引っ込ませる」処理で頂点と同じ数のいわば「補助頂点」を設定し、これと頂点とをジグザグに結ぶ、という方針である。 以下のように、まずまずの描画ができたが、正3角形だけは、何かヘンである。(^_^;)

void setup( )
{
	size(300, 300);
	background(255);
	smooth();

	noFill();
	star(3, 60, 75, 100, 100, -PI / 2.0, 0.50); // -90 degrees
	star(4, 170, 75, 25, 0.50);  // use simpler call

	fill(255, 204, 255);
	stroke(128, 0, 128);
	star(5, 60, 200, 75, 50, -PI / 2.0, 0.50); // -90 degrees

 	noFill();
	stroke(0);
 	star(6, 170, 200, 50, 100, 0, 0.50);
	stroke(128);
  
	// draw enclosing ellipses to make sure we did it right
	ellipse(60, 75, 100, 100);
	ellipse(170, 75, 50, 50);
	ellipse(60, 200, 75, 50);
	ellipse(170, 200, 50, 100);
}

void star(int n, float cx, float cy, float r, float proportion)
{
	star(n, cx, cy, 2.0 * r, 2.0 * r, 0.0, proportion);
}

void star(int n, float cx, float cy, float w, float h,
	float startAngle, float proportion)
{
	if (n > 2)
		{
			float angle = TWO_PI/ (2 *n);  // twice as many sides
 			float dw; // draw width
			float dh; // draw height
			w = w / 2.0;
			h = h / 2.0;
  			beginShape();
			for (int i = 0; i < 2 * n; i++)
				{
					dw = w;
					dh = h;
  					if (i % 2 == 1)
						{
							dw = w * proportion;
							dh = h * proportion;
  						}
					vertex(cx + dw * cos(startAngle + angle * i),
					cy + dh * sin(startAngle + angle * i));
				}
			endShape(CLOSE);
		}
}

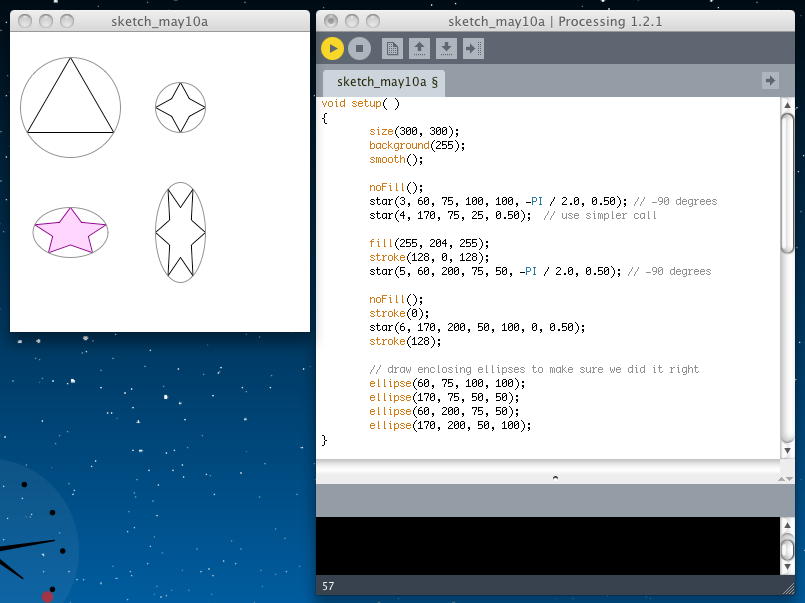
次のトピックは「何が悪かったのか」である。 上の例では、正3角形だけが、何かヘンであった。 これは、中心角の半分のところで、半径方向に一定の割合(propotion)で「引っ込ませる」処理で頂点と同じ数のいわば「補助頂点」を設定し、これと頂点とをジグザグに結ぶ、というその「propotion」が、なんとなく「0.5」に設定されていたからである。 半分もへっこんでいれば星形になるだろう・・・というのが甘かった。 以下のように、正3角形では、ちょうど辺の上がpropotion=0.5の場所であったのだ。

これを改良するには、正3角形では0.5より小さな値を指定すればよい。 以下の例では、いろいろなとんがりの星形が出来た。

void setup()
{
	size(300, 300);
	background(255);
	smooth();

	noFill();
	star(3, 60, 75, 100, 100, -PI / 2.0, 0.3); // -90 degrees
	star(4, 170, 75, 25, 0.5);  // use simpler call

	fill(255, 204, 255);
	stroke(128, 0, 128);
	star(5, 60, 200, 75, 50, -PI / 2.0, 0.75); // -90 degrees

	noFill();
	stroke(0);
	star(6, 170, 200, 50, 100, 0, 0.4);
	stroke(128);
  
	// draw enclosing ellipses to make sure we did it right
	ellipse(60, 75, 100, 100);
	ellipse(170, 75, 50, 50);
	ellipse(60, 200, 75, 50);
	ellipse(170, 200, 50, 100);
}

void star(int n, float cx, float cy, float r, float proportion)
{
	star(n, cx, cy, 2.0 * r, 2.0 * r, 0.0, proportion);
}

void star(int n, float cx, float cy, float w, float h,
	float startAngle, float proportion)
{
	if (n > 2)
		{
			float angle = TWO_PI/ (2 *n);  // twice as many sides
 			float dw; // draw width
			float dh; // draw height
			w = w / 2.0;
			h = h / 2.0;
  			beginShape();
			for (int i = 0; i < 2 * n; i++)
				{
					dw = w;
					dh = h;
  					if (i % 2 == 1)
						{
							dw = w * proportion;
							dh = h * proportion;
  						}
					vertex(cx + dw * cos(startAngle + angle * i),
					cy + dh * sin(startAngle + angle * i));
				}
			endShape(CLOSE);
		}
}

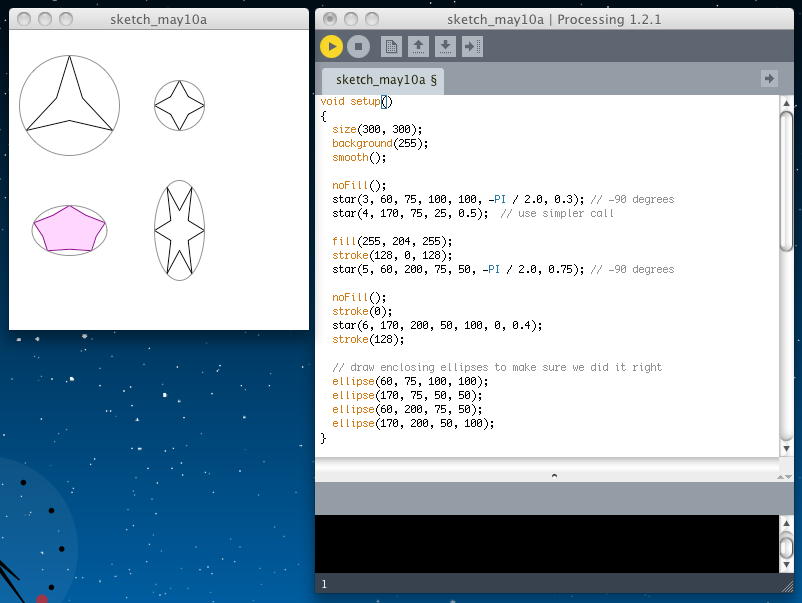
次がこの章の最後のトピック、「Using the Functions」である。 この章で見てきたように、ソフトウェア部品としての関数を作ることで、いろいろな複雑なグラフィクスも基本要素の組み合わせとして実現できる、 という事である。 これが、プログラミングなのである(^_^)。

以下の例では、ここまでに作った「polygon()関数」と「star()関数」を使って、リアルタイムにランダムな場所に色々な正多角形や星形を描画する、というなかなかゴージャスなプログラムとなっている。 アプレットとして書き出してみると、このようになった。

void setup()
{
  size(300, 300);
  background(255);
  frameRate(6);
  smooth();
  rectMode(CENTER);
}

void draw()
{
	// choose a random stroke color
	int r = int(random(0, 255));
	int g = int(random(0, 255));
	int b = int(random(0, 255));
	// and fill opacity
	int opacity = int(random(100, 255));
	int nSides = int(random(3, 9));
  
	// determine the center x and y coordinates
	int cx = 25 + 50 * int(random(0, 6));
	int cy = 25 + 50 * int(random(0, 6));
  
	// if a random number (0 or 1) is 0, draw a polygon;
	// otherwise, draw a star
	boolean isPolygon = int(random(2)) == 0;
  
	// for stars, you need the proportion of short to long radius
	float proportion;
  
	stroke(255); // erase any previous drawing in this area
	fill(255);
	rect(cx, cy, 50, 50); 
    
	stroke(r, g, b);
	fill(r, g, b, opacity);
	if (isPolygon)
		{
			polygon(nSides, cx, cy, 24);
		}
	else
		{
			proportion = random(0.2, 0.8) * cos(PI / nSides);
			star(nSides, cx, cy, 24, proportion);
		}
}

void polygon(int n, float cx, float cy, float w, float h, float startAngle)
{
	if (n > 2)
		{
			float angle = TWO_PI/ n;
			w = w / 2.0;
			h = h / 2.0;
			beginShape();
			for (int i = 0; i < n; i++)
				{
					vertex(cx + w * cos(startAngle + angle * i),
					cy + h * sin(startAngle + angle * i));
				}
			endShape(CLOSE);
		}
}

void polygon(int n, float cx, float cy, float r)
{
	polygon(n, cx, cy, r * 2.0, r * 2.0, 0.0);
}

void star(int n, float cx, float cy, float r, float proportion)
{
	star(n, cx, cy, 2.0 * r, 2.0 * r, 0.0, proportion);
}

void star(int n, float cx, float cy, float w, float h,
	float startAngle, float proportion)
{
	if (n > 2)
		{
			float angle = TWO_PI/ (2 *n);  // twice as many sides
 			float dw; // draw width
			float dh; // draw height
			w = w / 2.0;
			h = h / 2.0;
  			beginShape();
			for (int i = 0; i < 2 * n; i++)
				{
					dw = w;
					dh = h;
  					if (i % 2 == 1)
						{
							dw = w * proportion;
							dh = h * proportion;
  						}
					vertex(cx + dw * cos(startAngle + angle * i),
					cy + dh * sin(startAngle + angle * i));
				}
			endShape(CLOSE);
		}
}

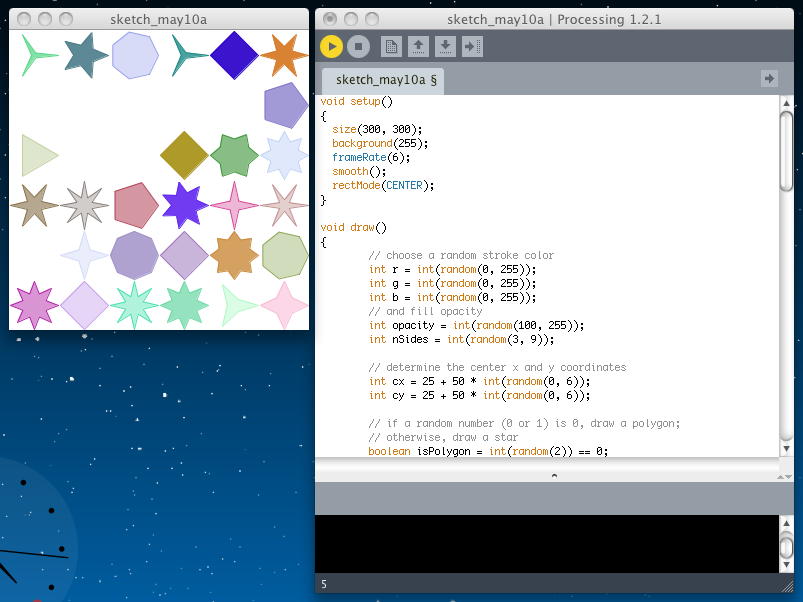
これでこのセクションは終わりである。 次回は チュートリアル のいよいよ最後、 Processing in Eclipse からという事になる。

2011年5月23日(月)

前回の日記から、また2週間も空いてしまった。 この間、 京都に行ったり とか NIME2011の準備 とか 突発の旅行 ーとかいろいろあった。 しかし「音楽情報科学」の講義で紹介したり、2人の院生(M1)に対してもProcessingの勉強が始まったので、 なんとしても進展していかなければならない(^_^;)。 SuperCollider日記 の方はもう1ヶ月半も放置しているが、これはオスロに向かう機内でやることとして、やはりProcessingからである。

前回の続きとして、今日は チュートリアル のラスト、 Processing in Eclipse である。

EclipseとはJava環境での「何か」であるらしいが、これを書きながら同時進行で Processing in Eclipse を読み進めているので、この時点ではまったく未知である。 これはEclipseのチュートリアルではない、とあるが、それでも「basics to get you up and running with Processing in Eclipse」をカバーしているそうである。 まずはEclipseをダウンロードしてインストールして、新しいプロジェクトを作り、Processingのライブラリをインポートして・・・・といろいろやっていく必要があるという。

第1ステップは「Download and install Eclipse」である。 まずは ここ に行ってみると、以下のようにたくさんある。 ますますEclipseとは何なのか、謎である。

この中の「Eclipse IDE for Java Developers」を選んで進め、とあるが、果たしてMacOSXの「32Bit」なのか「64Bit」なのか、謎である(^_^;)。 とりあえず対応していなければ警告されると予想して、「64Bit」を選んでみると、 筑波のミラーサイトが紹介されて、1分ほどで100MBほどのtar.gzファイルがゲットできた。 これを解凍すると、以下のようにIDE一式が出現した。

とりあえずこのフォルダをアプリケーションフォルダに入れ、eclipseアブリを起動してみた。 するとターミナルウインドウが出て(これは消えない(^_^;))、さらにデスクトップに「eclipse」というフォルダが現れ、 ワークスペースのディレクトリの設定を求められ、その後、以下のように何やらたくさん設定されて、eclipse画面が起動した。 大文字のEでなく、小文字で始まるeclipseというのが正しい?らしい。

このeclipse画面には以下のように、OverviewからSamplesまで一式ある。 Processingから枝分かれして、またもや巨大ジャングルに遭遇したようである(^_^;)。

第2ステップ「Create a new project」として、この「Java - Eclipse」ウインドウ(Welcome Screen)をいったんcloseせよ、という。 しかし「Exit?」というメッセージが出て、OKしたら何やらエラーで叱られた(^_^;)。 仕方ないので再びeclipseを起動して、「FILE --> NEW PROJECT and select "Java Project"」とした。 そして以下のようにプロジェクト名を適当に入れて「finish」すると、これでWelcome Screenに戻ったが、もう何もしない。謎である。(^_^;)

第3ステップは「Import the Processing libraries」とある。どうやらEclipseはそれ自体で閉じた体系であるらしく、 最初の状態ではEclipseはProcessingの事を何も知らない、という。 そこで、一つの方法としては、 このチュートリアル に従って、「pointing Eclipse to Processing's "lib" directory」とする方法があるという。 また別の方法としては、「CVSを経由して」(おいおい、いきなりCVSって何???(^_^;))、「copy the necessary Processing files into the project folder itself」ということで両者で共有する方法があるという。

ここまで来て、なんか嫌な予感がしてきた。 どうやらEclipseというのは、10数年前、かつてjava.sun.comのサイトから入手して、 日本語のJava本が1冊も出ていないJava黎明期に僕が独学でJavaを学んだ、あのJDK(Java Developer's Kit)の発展系のIDEなのではないか。 とすれば、このまま乗っていけば、それはProcessingを離れて、Javaの世界に限りなく突入することになる。(^_^;)

そこで、 Processing in Eclipse をいったん離れて、eclipseのWelcome Screenに戻って「Overview」を見てみると、以下のようなメニューである。

左側の5つは詳細不明なので、とりあえず右の「Java Development」をクリックしてみると、ブラウザが別ウインドウを開き、 以下のような壮大な世界が出現した。 ここで確信したが、「jar」とか「core」とか、要するにeclipseというのは、Processingという世界よりもずっと巨大なものなのだった。 JDKとはJavaベースでの統合Java開発環境だが、どうもこれが10数年のうちに相当に肥大していたのだ。

Processing in Eclipse のさっきの「Step 3. Import the Processing libraries」に続いて、「Step 4. Create a class and write your code!」があり、 そして「Step 5. Run!」とある。 ここで行っているのは、「Go to: RUN --> RUN AS --> JAVA APPLET」である。 つまり、このeclipseとProcessingとを繋ぐと、Processingのブラックボックスの裏にあった、Javaそのものから触れる、 ということである。 出て来るのはJavaアプレットであり、それはProcessingでもexportできる。

・・・ということで、ここで「深入り」の中断を決定した。 Processingをいろいろやって、もっと必要が出て来たらやってくるにしても、 「Processingって何だろう」という段階で入り込むことは無いのである。 これで晴れてようやく、 チュートリアル が全部、終わったことになる。 この次としては、以下のようなアドバンスのチュートリアルがあるという。 Webでなく「本」というものもある模様だが、これはぼちぼち、というところかなぁ。

• Tutorials on the Processing Wiki
• Getting Started with Processing and Data Visualization
• 3D Printing
• Media Processing
• The Nature of Code

ここでとりあえず「OSCでProcessing」というテーマに移ることにした。 Processingのサイトから「open sound control」をサーチすると、 こんな結果 となった。 なかなか有望な単語が見えているが、このサイトは2010年6月に終了したという。 新しいフォーラムは ここ であり、そこで再び 「open sound control」をサーチすると、 こんな結果 となった。 とりあえずソソられるところとしては、 using maxmsp to control processing? とか Processing ⇔ iPhone TouchOSC とか Controlling sketch variables with a Midi Keyboard, Joypad or other HID とかがある。 次には、ここからスタートしてみよう。

2011年5月26日(木)

午後には学科会議、そして教授会があり、その後に「くるる」で浜松駅に行き、e-wingでセントレアに向かう・・・というこの日、 午前中にぽっかりと時間が空いたので、受託研究に関するメイルとかも行き来しているが、ちょっとProcessingを進めてみることにした。 明日の朝のフライトでセントレア→成田→ミュンヘン→オスロ、と飛んで、 NIME2011 に行って、今年はコンサートセッションで入選したので、 去年12月のロシア で初演した、 この作品 を公演してくる予定なのだが、 なんと今週になってアイスランドで以下のようにまた噴火があり、フライトが正常に行くかどうかは微妙である。(^_^;)

Processingについては基本的には「ほぼ全貌をざっくり撫でた」ところなので、 最後のトピックは「OSCでMax5やSuperColliderと連携する」という部分である。 前回、リンクから見つけた新しいフォーラムは ここ であり、そこで「open sound control」をサーチすると、 こんな結果 となった。 そして、まさに直球の話題は using maxmsp to control processing? である。ここからスタートしていこう。

ここでの質問は以下のように「MaxMSPでProcessingをコントロール出来る?」というものである。

using maxmsp to control processing?

Hello

I would like to use processing to playback movies, however I would like 
to use the interface I made in maxMSP (basically 5 buttons)to control 
the playback. I want to use processing because the framerate drops fast.
Can anyone put me on the right track? the scheme is:
MaxMSP to start playback, processing to do the playback (video and sound).

そして2人がそれぞれ「こうすれば?」とのアドバイスを述べていて、あと1人が、 おそらく試したProcessingプログラムがうまく動かない?というカンジで質問しているが、 これは誰にもフォローされず放置されている(^_^;)。

第一のコメントは質問が書かれて2時間後である。なかなかアクティブなコミュニティのようだ。

Hi sam,

I usually use ur setup and I do it with the UDP protocol.
maxmsp (udpsend object to send signal to an IP)
processing (UPD library by Stephan Cousot to receive the signal)

use the same ip for the sending (in max) and the receiving (in p5)

そしてもう一つのコメントも、質問が書かれた翌日に書かれていた。

You could check out the oscP5 library
and the related open sound control objects in max

それぞれのリンク先はちょっと違うが、いずれもOSC、それも「P5」というのがどうやらキーワードである。 僕がOSCを使ったのはだいぶ昔、 GDS (global delayed session) Music の時(2002年 - 9年前(^_^;))だったので、OSCもだいぶ進化しているだろうから、 まずはMax5側からOSCの復習をする必要がありそうだ。

上記の2つの「ProcessingとOSC」のリンクにいきなり進むのをグッとこらえて、まずはMax5でのOSCである。 遠い記憶によれば、スタンフォード大のCNMATで開発提唱されたOSCだが、これは別に技術的に目新しいものというより、 プロトコルとして「汎用」に主眼を置いたものなので、MaxがMax5になる以前に、エクスターナル(外部拡張)標準オブジェクトでなく、 Max5の標準オブジェクトとして取り込まれて提供されていた筈である。 まずはここから確認していこう。

とりあえずMax5を起動して、ヘルプに「udp」と入れてみた。 OSCとはUDPプロトコルを使ったネットワーク情報交換システムなので、たしか「udpsend」「udpreceive」とかだった記憶がある。 すると以下のように、メニューに「UDP Tester」というのがある。 Max5のこういうツールは当然ながらMax5で書かれているので、これを改造すれば、仕組みが判る筈である。

「UDP Tester」を起動してみると、なんとこのツールはedit出来ないようになっていた(^_^;)。 確かそれを外す方法があったが、とりあえず動かしてみると、ちゃんとローカルホストの「127.0.0.1」でメッセージがsendされ、 receiveされていた。 さらにこの中には「jit.net.send」と「jit.net.recv」と「audio over network」というボタンがあり、 前者2つを開いてみると、以下のように、jitterのオブジェクトとして、UDPでなくTCP/IPベースでのsend/receiveと、 さらにオーディオ信号をTCP/IP上で転送するような環境も出来ていた。これは凄い。(^_^)

ただし、ここではProcessingやSuperColliderと連携するので、TCP/IPでなくUDPのOSCでないと困るので、 ここもグッとこらえて、とりあえずMax5パッチとして「udpsend」を置いて、以下のようにヘルプを引いてみた。 「udpsend」と「udpreceive」は必ずペアになるので、ヘルプパッチはタイトル以外は同一だった。

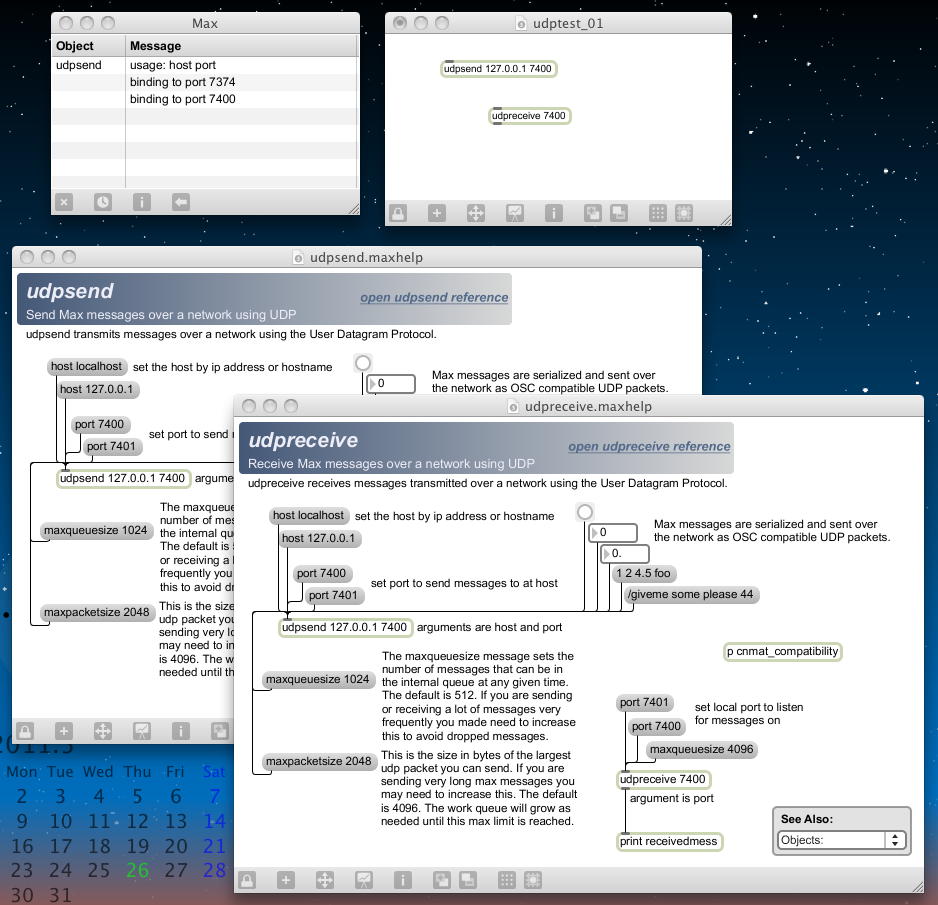
GDS (global delayed session) Musicのように、 ネットワークに繋がれた複数のコンピュータで通信(連携)しながら何かする場合には、 それぞれのパソコンできちんとIPアドレスを設定した上で、それぞれのポートを規定してやりとりする。 でも当面は、1台のコンピュータの内部で、Max5とProcessingとSuperColliderとを同時に走らせて、 それらの相互通信にOSCを使うだけなので、ここではIPアドレスはlocalhost(127.0.0.1)のままで行くことにした。 ただし、ポート番号はせっかくなのでサンプルとは変えていこう。

そこでまずは、 udptest_01.maxpat というパッチを作って以下のように走らせて、 GDS (global delayed session) Music の時代のものと変わっていない(正確にはCNMATのOSCと互換である)ことを確認した。 この例でMaxウインドウにポート番号が出て来るのは、「udpreceive」が呼ばれたりそのポート番号が設定された時だけである。

これでMax5側の確認は出来たので、いよいよProcessingフォーラムの最初のコメントで紹介された、 UPD library に行ってみよう。 ここは以下のような内容となっている。

ここで、「README」を見るとあまり大したことは書かれておらず(^_^;)、「documentation/」を見ると、 この「/shared/processing/udp」には、

• java
• picoip
• udp

の3種類がある事が判る。 とりあえずはUDPに限定するために、「picoip.zip」はゲットしない事にする。 また「previous_version/」というのは試作段階の旧バージョンなのでこれも無視。 まずゲットするのは udp.zip である。 これを解凍して調べてみると、 UPD library で他にある「documentation/」と「examples/」の中身も、以下のようにローカルで全て入っていたので、 これで十分である。

さて、ここまでくればとりあえずサンプルを実行である。 「examples/udp」の下には、「udp.pde」と「udp.pd」の2つのファイルがある。 「.pde」はProcessingのスケッチである。「.pd」はテキストファイルだが、以下のように、 テキストセーブしたMaxパッチに似ているものの、これはPd(PureData)ソースであり、 互換性が無いので使えない。(^_^;)

#N canvas 103 333 764 337 10;
#X obj 36 28 cnv 15 690 190 empty empty empty 20 12 0 12 -237178 -212212
0;
#X obj 36 221 cnv 15 690 70 empty empty empty 20 12 0 14 -146177 -66577
0;
#X obj 45 256 print receive;
#X text 177 233 <-- Opens a socket for UDP network reception on port
6100 and prints the received message.;
#X obj 47 116 netsend 1;
#X msg 47 94 disconnect;
#X floatatom 47 164 5 0 0 0 - - -;
#X text 95 164 <-- Reports whether the connection is open or not (0=close
\, nonzero otherwise).;
#X obj 242 70 cnv 15 480 60 empty empty empty 20 12 0 14 -259904 -66577
0;
#X msg 249 100 send \$1;
#X floatatom 249 82 5 0 0 0 - - -;
#X obj 45 234 netreceive 6100 1;
#X msg 47 72 connect localhost 6000;
#X text 314 81 [2] Send the current number to the remote machine (change
the value by dragging the number box or type directly the new value).
;
#X text 47 40 [1] Connect to 'localhost' on port 6000 for sending UDP
messages.;
#X connect 4 0 6 0;
#X connect 5 0 4 0;
#X connect 9 0 4 0;
#X connect 10 0 9 0;
#X connect 11 0 2 0;
#X connect 12 0 4 0;

そこで「udp.pde」をダブルクリックして実行すると、Processingが起動し、以下のようにProcessingウインドウが開いた。 解説のコメントが全て入ったオリジナルのソースは これ である。 ところが実行するとエラーが出た。(^_^;)

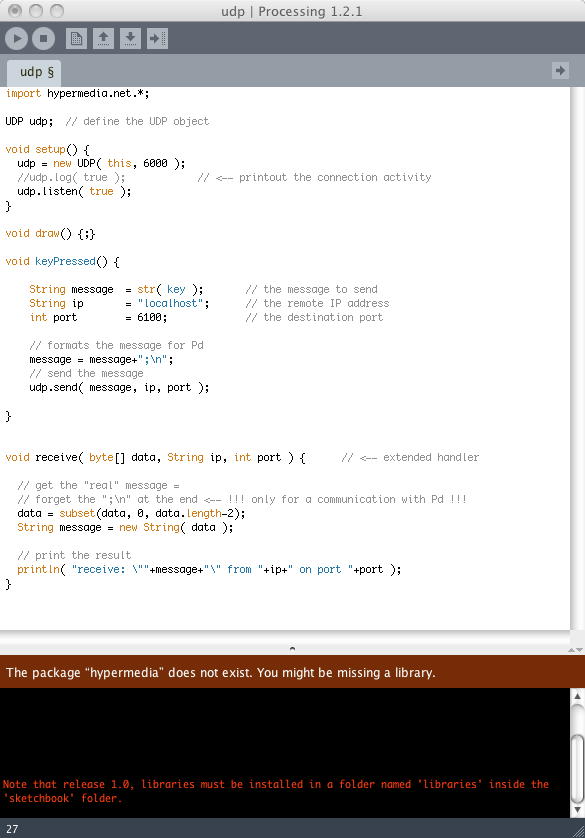
エラーの原因は明確である。 ソースの冒頭の

import hypermedia.net.*;

という、肝心のライブラリが無いのである(^_^;)。 これはパソコンを検索しても出てこないので、ここでこの第一のアドバイスの路線での探求については断念である。

次の、というか最後の候補は、 oscP5 library ということになる。 しかし、このサイトはなかなかに充実している。 だいたい、きちんと、 OpenSound Control Home Page のリンクがあるところからして、安心できる(^_^)。

まずはこのサイトの「Download」のところから、 oscP5 version 0.9.6 release 05/09/2010 をダウンロードして解凍してみると、以下のようになっている。

ここにある「INSTALL.txt」が、以下のようになかなか親切である。 とりあえずはこれに従ってやってみよう。

Find instructions on how to install library oscP5 below.

Where do I find my Processing sketchbook folder?
You can find the location of your sketchbook in the 
Preferences menu item inside your Processing application.
By default the following locations are used:
for mac users the sketchbook folder is located inside ~/Documents/Processing. 
for windows users the sketchbook folder is located 
inside folder 'My Documents'/Processing

in the following folder structure, Processing refers to your 
sketchbook folder. Put library oscP5 into the 'libraries' folder 
inside your sketchbook folder. 
if folder 'libraries does not exist, create it.

Processing
  libraries
    oscP5
      examples
      library
        oscP5.jar
      reference
      src
                      
after library oscP5 has been successfully installed, restart processing.

要するに、ここで「oscP5.zip」を解凍した「oscP5」というフォルダを、Processingのプリファレンスで定義した 「Processing」フォルダの下の「libraries」フォルダの下に置けばいいのである。 ・・・とすれば、さきに断念した第一のパターンもこれをしたら動きそうだが、混乱するのでとりあえず後回しにしよう。(^_^;)

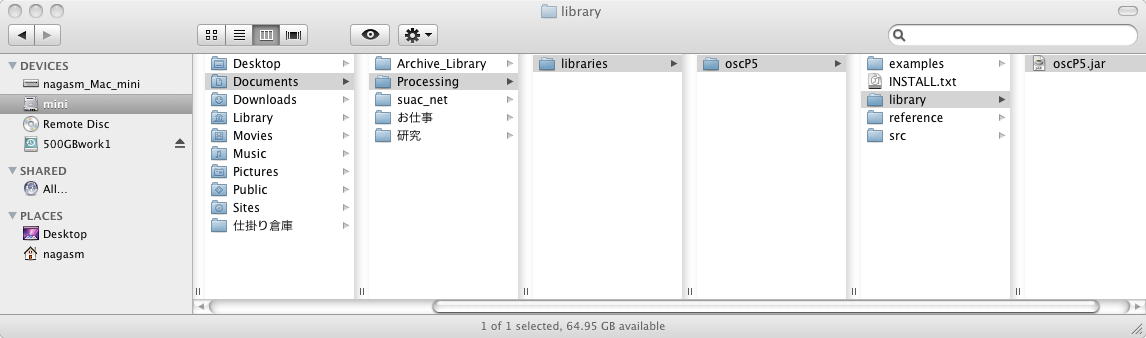
ここで、「example」フォルダの中のProcessingサンプルを起動して実行してみると、エラーが出なかった。 つまり、何らかのUDP通信が出来ているのでは・・・と思われるが、ここでお昼休みとなった(^_^;)。 午後は会議、そして出発ということで、今日はここまでである。続きは帰国後、だいぶ先になりそうだ。

Processing日記(4)

「日記」シリーズ の記録