---

Processing日記(2)

長嶋 洋一

(一部　SuperCollider日記かも)

　Part 1　 　Part 3　 　Part 4　 　Part 5　

---

2011年3月19日(土)

前回の日記が3月5日で、もう2週間も空いてしまった。 その経緯は SuperCollider日記 の方にあるので省略して、忘れない程度に少しでも着手することにした。 前回は チュートリアル の Images and Pixels までやったので、今日は Drawing Curves からである。 イラストレータやFlashで重要な、いろいろな曲線をベクター形式で描画する、というものである。

曲線のタイプの最初は「Arcs」である。これは矩形に内接する楕円として定義し、始点と終点を角度で指定する。 角度については「PI」という定数がラジアンとして予約されている。 パラメータは

arc(x, y, width, height, start, stop);

と定義される。 以下の例では、4つの矩形を描いて、それぞれに内接する曲線を描画している。 1回、描画するだけなので「setup()」の中だけである。

void setup()
{
	size(300, 200);
	background(255);
	smooth();
  
	rectMode(CENTER); // show bounding boxes
	stroke(128);
	rect(35, 35, 50, 50);
	rect(105, 35, 50, 50);
	rect(175, 35, 50, 50);
	rect(105, 105, 100, 50);
  
	stroke(0);
	arc(35, 35, 50, 50, 0, PI / 2.0); // lower quarter circle 
	arc(105, 35, 50, 50, -PI, 0);  // upper half of circle
	arc(175, 35, 50, 50, -PI / 6, PI / 6); // 60 degrees
	arc(105, 105, 100, 50, PI / 2, 3 * PI / 2); // 180 degrees
}

次の曲線のタイプは「Spline Curves」である。正しくは「Rom-Catmull Spline」と言う。 定義は以下である。

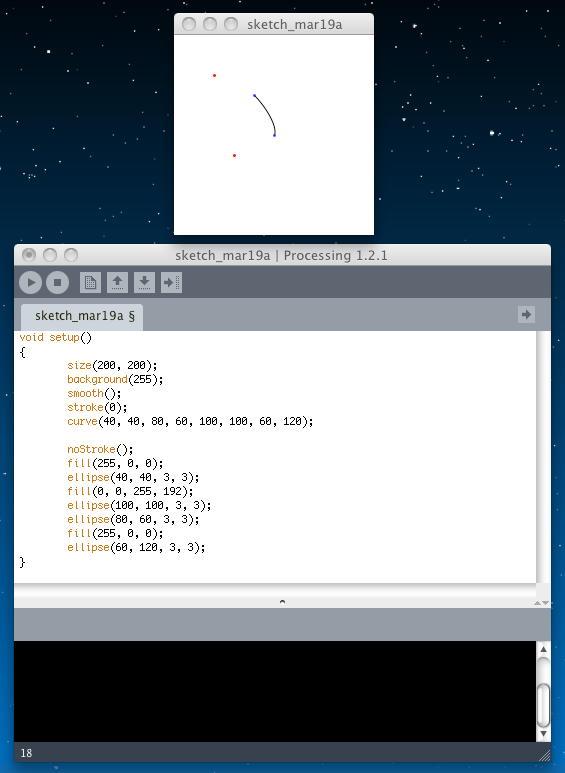
curve(cpx1, cpy1, x1, y1, x2, y2, cpx2, cpy2);

cpx1, cpy1	Coordinates of the first control point
x1, y1		Coordinates of the curve’s starting point
x2, y2		Coordinates of the curve’s ending point
cpx2, cpy2	Coordinates of the second control point

曲線に作用するこの2つのコントロールポイントと始点・終点の意味と位置関係は、

• The tangent to the curve at the start point is parallel to the line between control point one and the end of the curve. These are the lines shown in green in the diagram at the left.

• The tangent to the curve at the end point is parallel to the line between the start point and control point 2. These are the lines shown in purple in the diagram at the left.

とある。 ここの説明 で実際に体験してみるとよく判る。 以下の例では、始点・終点・2つのコントロールポイントも描画している。

void setup()
{
	size(200, 200);
	background(255);
	smooth();
	stroke(0);
	curve(40, 40, 80, 60, 100, 100, 60, 120);
  
	noStroke();
	fill(255, 0, 0);
	ellipse(40, 40, 3, 3);
	fill(0, 0, 255, 192);
	ellipse(100, 100, 3, 3);
	ellipse(80, 60, 3, 3);
	fill(255, 0, 0);
	ellipse(60, 120, 3, 3);  
}

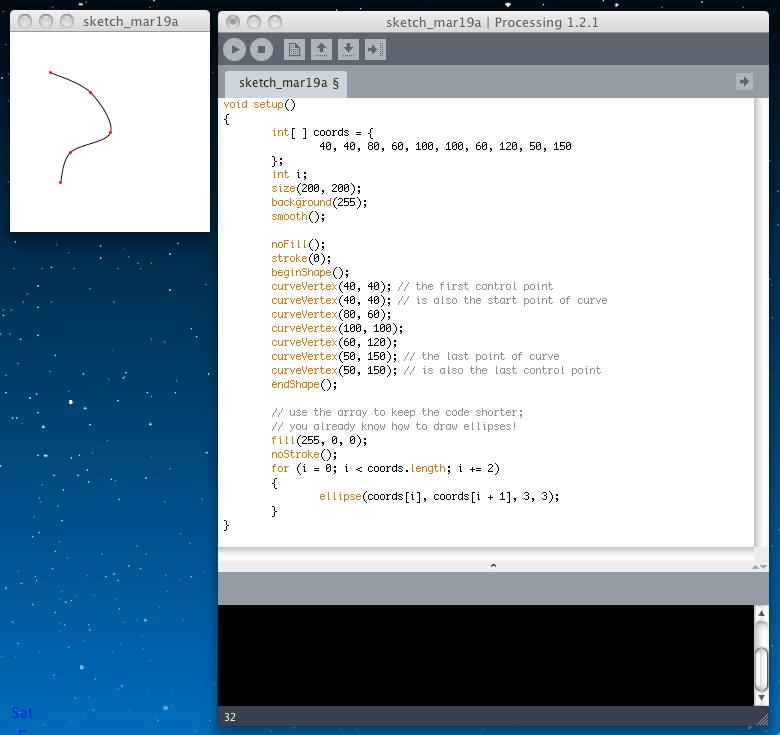
次の曲線のタイプは「Continuous Spline Curves」である。 上記の単独のスプライン曲線を組み合わせて、思ったような曲線を実現するのは現実的ではないので、こちらが有効な方法である。 まず最初に「beginShape()」関数を置き、そこから「curveVertex()」を次々に記述する。 最後に「endShape()」関数で閉じることになる。 以下の例でも、始点・終点・2つのコントロールポイントを描画している。

void setup()
{
	int[ ] coords = {
		40, 40, 80, 60, 100, 100, 60, 120, 50, 150
	};
	int i;
	size(200, 200);
	background(255);
	smooth();

	noFill();
	stroke(0);
	beginShape();
	curveVertex(40, 40); // the first control point
	curveVertex(40, 40); // is also the start point of curve
	curveVertex(80, 60);
	curveVertex(100, 100);
	curveVertex(60, 120);
	curveVertex(50, 150); // the last point of curve
	curveVertex(50, 150); // is also the last control point
	endShape();
  
	// use the array to keep the code shorter;
	// you already know how to draw ellipses!
	fill(255, 0, 0);
	noStroke();
	for (i = 0; i < coords.length; i += 2)
	{
		ellipse(coords[i], coords[i + 1], 3, 3);
	}
}

次の曲線のタイプは「Bezier Curves」である(実際にはBezの「e」にはチョンが付くが省略)。 これはアート的な曲線には必須である。 「bezier()」関数には以下のように6つのパラメータがあるが、何故かその順序が違っているので注意が必要である。

bezier(x1, y1, cpx1, cpy1, cpx2, cpy2, x2, y2);

x1, y1		Coordinates of the curve’s starting point
cpx1, cpy1	Coordinates of the first control point
cpx2, cpy2	Coordinates of the second control point
x2, y2		Coordinates of the curve’s ending point

このパラメータの意味は、 ここの説明 で実際に体験してみるとよく判る。 以下の例では、始点・終点・2つのコントロールポイントも描画している。

void setup( )
{
	size(150, 150);
	background(255);
	smooth();

	ellipse(50, 75, 5, 5); // endpoints of curve
	ellipse(100, 75, 5, 5);
	fill(255, 0, 0);
	ellipse(25, 25, 5, 5);  // control points
	ellipse(125, 25, 5, 5); 
	noFill();
	stroke(0);
	bezier(50, 75, 25, 25, 125, 25, 100, 75);
}

最後の曲線のタイプは「Continuous Bezier Curves」である。 上記の単独のベジェ曲線を組み合わせて、思ったような曲線を実現するのは現実的ではないので、こちらが有効な方法である。 まず最初に「beginShape()」関数を置き、そこから「vertex(startX, startY)」を次々に記述する。 最後に「endShape()」関数で閉じることになる。 定義は以下である。

bezierVertex(cpx1, cpy1, cpx2, cpy2, x, y);

cpx1, cpy1	Coordinates of the first control point
cpx2, cpy2	Coordinates of the second control point
x, y		The next point on the curve

これにより、上述のベジェ曲線は以下のようにも記述できる。

void setup( )
{
	size(150, 150);
	background(255);
	smooth();
	// don't show where control points are
	noFill();
	stroke(0);
	beginShape();
	vertex(50, 75); // first point
	bezierVertex(25, 25, 125, 25, 100, 75);
	endShape();
}

以下の例では、連続ベジェ曲線といってもスムースに接続されていない。

beginShape();
vertex(30, 70); // first point
bezierVertex(25, 25, 100, 50, 50, 100);
bezierVertex(50, 140, 75, 140, 120, 120);
endShape();

連続ベジェ曲線でスムースに接続されるためには、曲線Aの最後のコントロールポイントと、次の曲線Bの最初のコントロールポイントとが、以下のように一直線上に並ぶ必要がある。

beginShape();
vertex(30, 70); // first point
bezierVertex(25, 25, 100, 50, 50, 100);
bezierVertex(20, 130, 75, 140, 120, 120);
endShape();

これで曲線はおしまいである。 チュートリアル の Drawing Curves が終わったので、続きはまた後日。

2011年3月30日(木)

前回の日記が3月19日で、また10日以上も空いてしまった。 一昨日までの経緯は SuperCollider日記 の方にある。 また昨日は、卒展以来、懸案だった SUACインスタレーション(3) の改訂などしていたので、これも仕方ない。

今日は このように 新2回生5人が研究室を来訪してマルチメディア室/電子制御機器制作室の新しいMax5のインストール作業を手伝ってくれたり、 このように いよいよ修了制作を目指す新M2のアポ(Commゼミから大学院に進学した2人のアポはまた明日)もあったので、時間は少ししか作れなかったが、忘れない程度に少しでも進めることにした。

前回は チュートリアル の Drawing Curves までやったので、今日は Strings and Drawing Text からである。 Java言語ではいろいろな文字列とかテキストの処理が格段にC言語から向上したので、Java環境に乗っているProcessingでは、いろいろ簡単に文字情報を扱える、と期待できる。 モーションタイポグラフィーにも活用できるだろう。

まずは「The String class」である。 Processingで「文字」があれば、そこにはString classがある。 最初の以下のサンプルを実行したが、1行目は正しく実行され、2行目は「そんなjpgファイルは無い」と叱られた(^_^;)。

println("printing some text to the message window!");
  // Printing a String
PImage img = loadImage("filename.jpg");
  // Using a String for a file name

次に、String classについてのリファレンスは ここ だ、と紹介されている。 また、これはProcessingのカバーしている部分だけなので、完全にはJavaのサイトの ここ を見ろ、とあった。 ・・・まぁ、たぶん間違いなく、山のようにたくさんあるので、軽く無視しておこう。(^_^;)

ここでようやく「What is a String?」である。 要するに文字列とは、以下のような文字データの格納された配列である。 その末尾には自動的に、これでオシマイ、というnullストリングとしてデータ「0」が置かれる。 データ「0」は、文字(キャラクタ)コードではないので区別できる。 もし、Stringクラスを持たなければ、これは以下のように扱わなければならない。

char[] sometext = {'H', 'e', 'l', 'l', 'o', ' ', 'W', 'o', 'r', 'l', 'd'};

しかしProcessing(Java)では、以下のように「String」オブジェクトを定義するのが普通である。

String sometext = "How do I make String? Type some characters between quotation marks!";

これで判るように、Stringとはダブルコーテーションマークで囲まれた文字列というだけである。 なお内部的には、ここにも見えないが最後に「end of string」というデータがある。 このStringを参照する時には、先頭文字のポインタしか使わないので、文字列の長さは不明であり、最後のnullキャラクタが消えれば文字列の長さが不定となって暴走したりする(^_^;)。

ここで強調されているのは、Stringとは「methodを伴ったobjectである」という事である。 これは既に学んだ「PImage」が、画素データの集合体(配列)として、「copy()」とか「loadPixels()」とかで扱われるのと同様である。

一例として、以下の「charAt()」というメソッドは、与えられたインデックス(○文字目、という配列要素の指定。ただし先頭は1でなくゼロ)の文字を返す。 インデックスが「3」なので、3文字目の「m」でなく、4文字目の「e」を返している。

String message = "some text here.";
char c = message.charAt(3);
println(c);                // Results in 'e'

Stringの長さは可変長なので、その長さを取得する「length()」メソッドは重要であり役に立つ。 文字コードの配列の最後のnullキャラクタを探すのではなく、以下のようにStringオブジェクトの「length」というプロパティ(属性)を取得する関数として「length()」を呼び出す、というのが正しいマナーである。

String message = "This String is 34 characters long.";
println(message.length());

Javaは大文字と小文字を区別する文化である。 なので、Processingでも、以下のように、Stringを全て大文字に変換する「toUpperCase()」メソッド、Stringを全て小文字に変換する「toLowerCase()」メソッドがある。

String message = "This String is 34 characters long.";
String uppercase = message.toUpperCase();
println(uppercase); 
String lowercase = message.toLowerCase();
println(lowercase); 

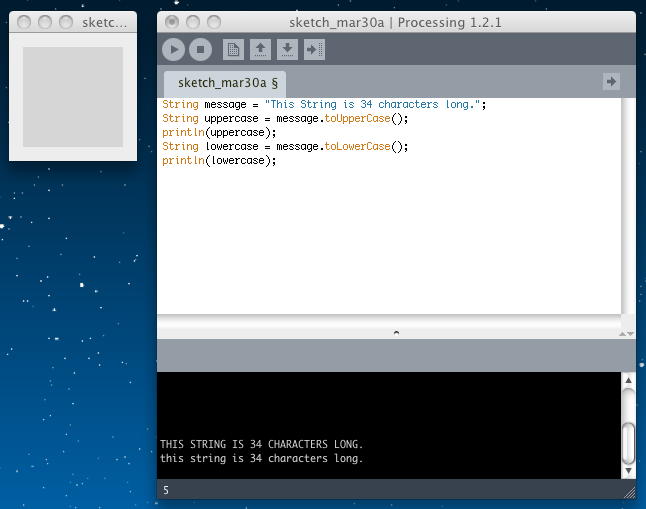
ここで、何故、いちいち新しいuppercaseというStringオブジェクトを定義して、それをprintlnで表示しているのか?　という疑問が出るのは当然である。 確かに、以下のように、直接でもちゃんと表示する。

String message = "This String is 34 characters long.";
println(message.toUpperCase()); 
println(message.toLowerCase()); 

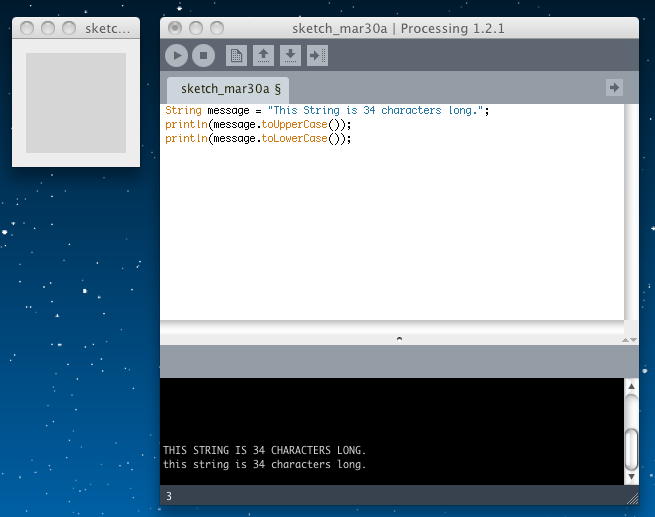
その疑問への回答としては、Stringは「immutable」(不変)という特別な種類のオブジェクトである、という事である。 immutableなオブジェクトとは、そのデータが変更できないものだという。 上の例では、「message」という名前のオブジェクトは変化しておらず、「message.toUpperCase()」というのは「toUpperCase()」というメソッドを適用した新しいオブジェクトが結果として得られるという。 確かに、以下のように、文字配列だと特定の文字を書き換えることが可能である。

char[] text1 = {'H', 'e', 'l', 'l', 'o'};
text1[0] = 'Z';
println(text1);

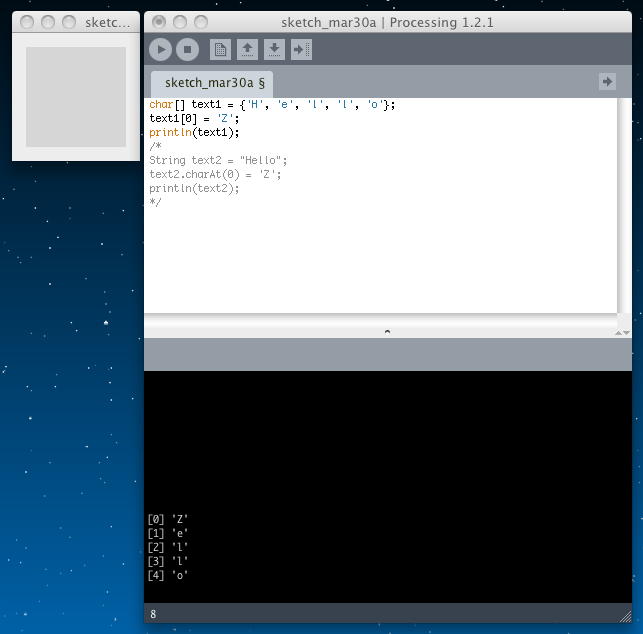
しかし以下のように、Stringオブジェクトの中の特定の文字を変更しようとしてもエラーが出て実行できない。これが「immutable」という事である。

String text2 = "Hello";
text2.charAt(0) = 'Z';
println(text2);

さて、ここで以下の例を見てみよう。 上の3行の部分では、「==」という演算子で「one」と「two」と定義されたストリング(中身はいずれも"hello")を比較している。その結果は一致しているということで「true」と出た。 下の3行の部分では、「equals()」というメソッドで「three」と「four」と定義されたストリング(中身はいずれも"hello")を比較している。その結果は一致しているということで「true」と出た。

String one = "hello";
String two = "hello";
println(one == two);

String three = "hello";
String four = "hello";
println(three.equals(four));

しかし実は、上の例のうち最初の3行は駄目なんだ、というのがここでの注意点である。 比較演算子「==」は、「one」と「two」と定義されたストリングのアドレス(ポインタ)を比較しているだけである。 たまたまこの例では、いずれも同一の文字列なので、コンパイラが気をきかせて「同じ場所だよ」と効率化を図ってくれたが、もし、それぞれのオブジェクトインスタンスが異なっていれば、メモリ内に配置されるアドレスは異なり、この結果は「false」となる場合もある。

これに対して、上の例の下の3行はOKである。 文字列比較メソッド「equals()」は、「three」と「four」と定義されたストリングの中身そのものを全てにわたって検索して比較し、完全に一致している時にのみ「true」を返すので、本当の意味での文字列の比較には、こちらを使わなければならない。

次のサンプルは「文字列の結合」である。 これはC言語の時代には、「文字列を結合する関数」などを呼び出すなど面倒だったが、Javaではなんと単純に

String helloworld = "Hello" + "World";

という書式を許すようになった。 これはURLを生成することを考えると、プログラミングが画期的に簡単になる事を意味した。 Processingではもちろん、これが使える。

さらにJavaでは、つまりProcessingでも、文字列と変数とを単純に連結(concatenation)できる。 これまた、C言語では「変数を文字データに変換する関数」とか「文字をASCIIコードとしてデータ化する関数」など、気の狂いそうな複雑な世界だったのに比べて、URL(連番のファイル名など)を生成することを考えると、プログラミングが画期的に簡単になる事を意味する。 以下の例がもっともシンプルなものである。 これはJavascriptなどでも踏襲されているので、今の若い学生はそんなものだと思うだけなのかな。(^_^;)

int x = 10;
String message = "The value of x is: " + x;
println(message);

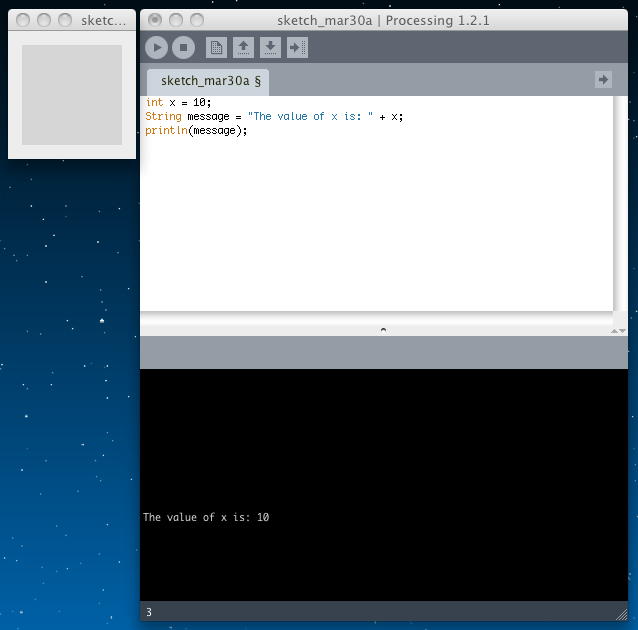
次のトピックは「Displaying Text」であるが、今日はここまで。

2011年4月1日(金)

今日はエイプリルフールだが、震災の影響でほとんどおちゃらけ/嘘Webサイトが見当たらない、安心の4月1日となった。 昨日は SuperCollider日記 をやったが、今日は昼前から出掛けて東京→土浦へ、そして明日は日立に行くのでほとんど進めない。 この日の分は、浜松から東京への新幹線と、上野から土浦までの常磐線の中だけで執筆した。

前回は チュートリアル の Drawing Curves の Strings and Drawing Text を途中までやったので、その続き、「Displaying Text」からである。

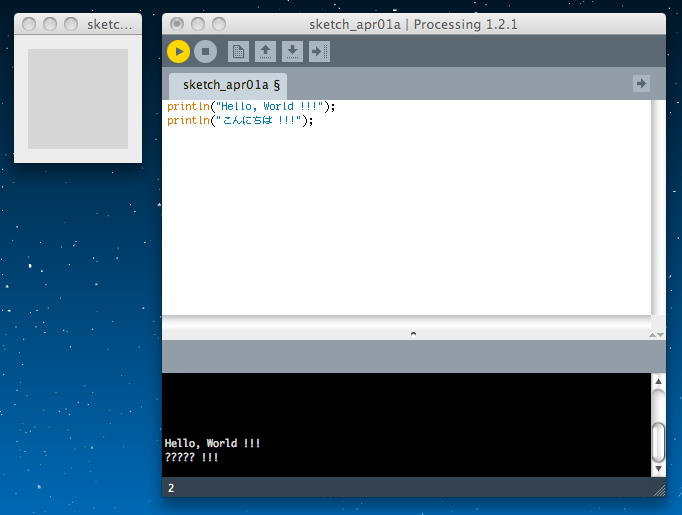
もっとも簡単な文字列表示は、以下のように、message windowに「println()」で表示する、という事である。 これはデバッグでも活躍する定番の情報出力である。 日本語はソースの中では見えたが、表示では化けた。 化けるような文字は、使わなければいいだけである。

println("Hello, World !!!");
println("こんにちは !!!");

デバッグ目的でなく、Processingのプログラムそのものがテキスト表示を行う場合には、以下のように6つのステップによってフォントの設定を行う。

STEP 1

まず以下のように、「"Tools" → "Create Font."」を選んで、Processingに固有の"vlw"という形式のフォントデータを登録する。

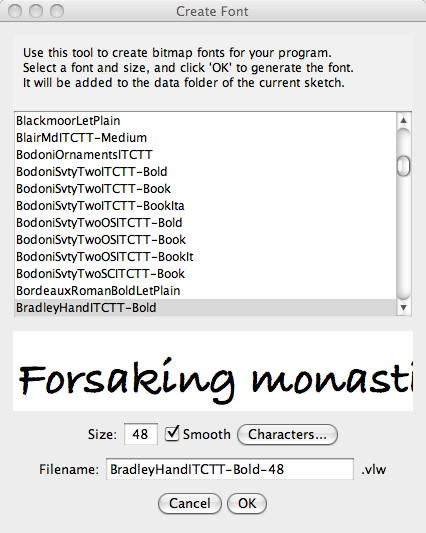
STEP 2

オブジェクトのタイプを「PFont」と指定するために、例えば変数fの定義は「PFont f;」とする。

STEP 3

ファイル名を指定して「LoadFont()」関数を使ってフォントを読み込む。この処理は「setuo()」の中で一度だけ行えばよい。「draw()」の中に入れると遅くなったりヘンな事が起きるので推奨しない。例えば「f = loadFont("Serif-48.vlw");」となる。

STEP 4

「textFont()」を使ってフォントを呼び出す。例えば「textFont(f,36);」となる。この2つの引数は、指定される変数と、そのフォントサイズである。

STEP 5

「fill()」を使って、そのフォントの色を指定する。例えば「fill(255);」となる。

STEP 6

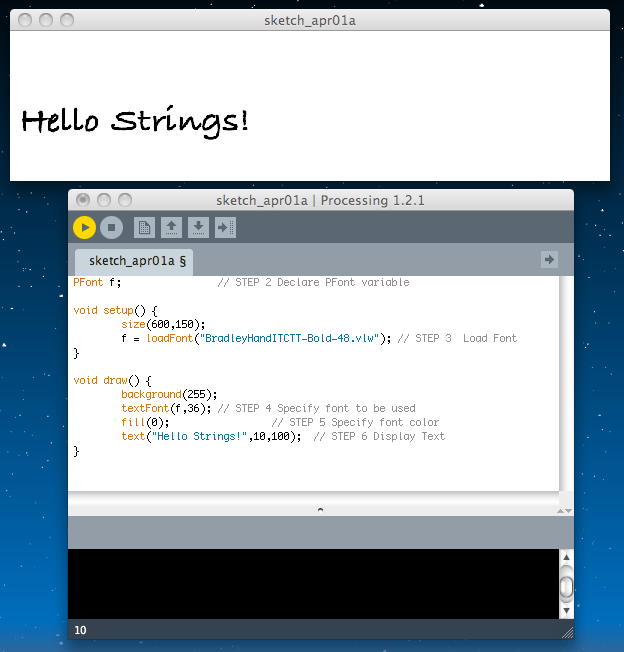
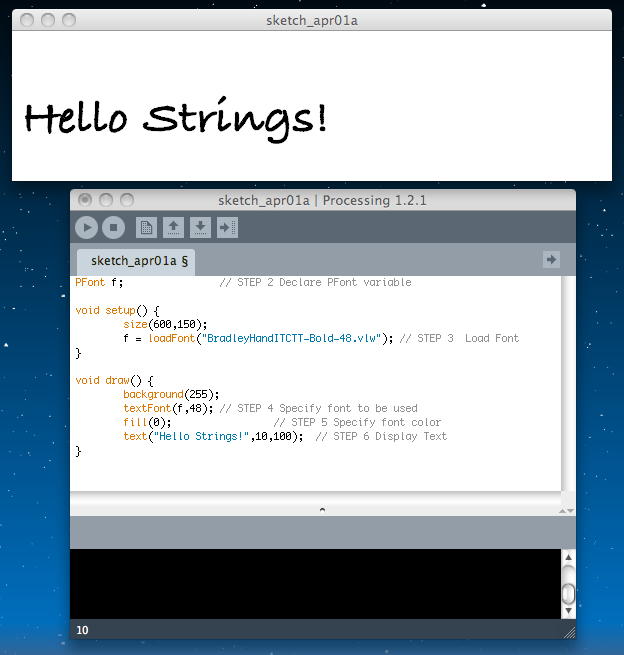
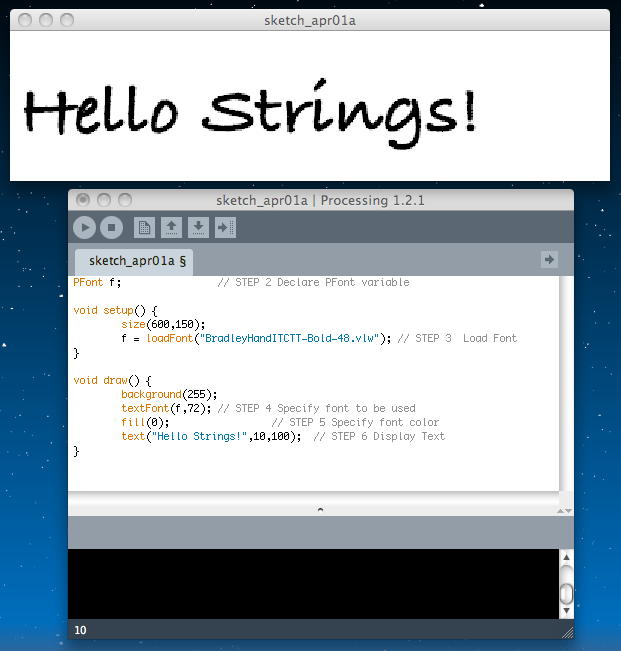
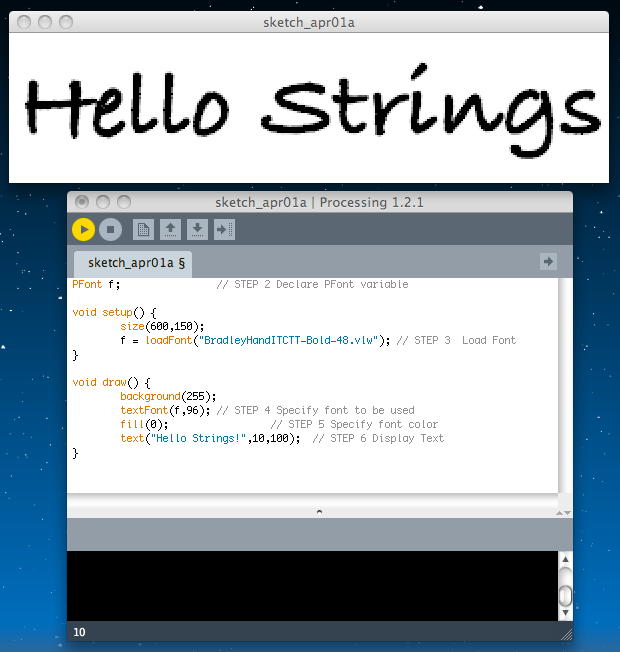
「text()」関数によってテキストを表示する。text()は3つの引数を持つ。1つ目がテキスト、2/3個目は表示する座標である。 例えば「text("Hello Strings!",10,100);」となる。

以下が、これをまとめた例である。いくつかのフォントサイズを指定してみたが、Flashのベクターフォントほど奇麗ではなく、そこそこにギザるようである。(^_^;)

PFont f;		// STEP 2 Declare PFont variable
  
void setup() {
	size(600,150);
	f = loadFont("BradleyHandITCTT-Bold-48.vlw"); // STEP 3  Load Font
}

void draw() {
	background(255);
	textFont(f,36);	// STEP 4 Specify font to be used
	fill(0);		 // STEP 5 Specify font color 
	text("Hello Strings!",10,100);	// STEP 6 Display Text
}

フォントは以下のように「createFont()」でも作ることができる。ただしこれは、ローカルマシンに登録されているフォントだけに限り、またリサイズなどに対応していないので推奨しない。available fontsは「PFont.list()」で参照できる。

f = createFont("Georgia", 24, true);

次のトピックは「Animating Text」である。モーションタイポグラフィなどこれはなかなか強力そうだ。 まず最初は「textAlign()」である。その意味は文字通り、「specifies RIGHT, LEFT or CENTER alignment for text」である。 以下のように、テキスト全体に対して、HTMLと同様に「程よく」配置してくれる。

PFont f;

void setup() {
	size(400,200);
	f = createFont("Arial",16,true); 
}

void draw() {
	background(255);
	stroke(175);
	line(width/2,0,width/2,height);
	textFont(f);       
	fill(0);
	textAlign(CENTER);
	text("This text is centered.",width/2,60); 
	textAlign(LEFT);
	text("This text is left aligned.",width/2,100); 
	textAlign(RIGHT);
	text("This text is right aligned.",width/2,140); 
}

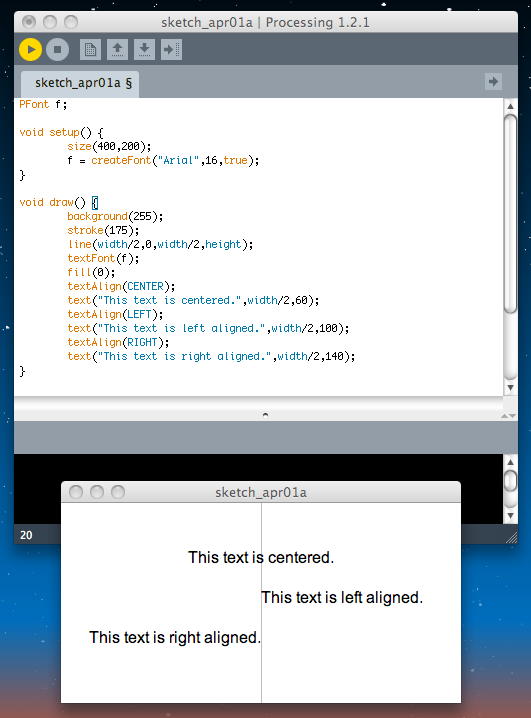
次は「textWidth()」である。これは「Calculates and returns the width of any character or text string」という、なかなか強力な機能だ。これは、以下の例のように、ニュース速報のように文字列が画面を横スクロールする場合に、画面の幅と表示文字列の幅を比較したりするのに便利である。 ここでは、表示位置のx座標を毎回「-3」していて、マイナスにまで進んでいくが、スクリーンから見切れて表示されていなくても内部的にはその移動が続いている、というのがポイントである。

String[] headlines = {
	"Processing downloads break downloading record.", 
	"New study shows computer programming lowers cholesterol.",
};

PFont f;  // Global font variable
float x;  // horizontal location of headline
int index = 0;

void setup() {
	size(600,100);
	f = createFont("Arial",36,true);  
	x = width; 
}

void draw() {
	background(255);
	fill(0);
	textFont(f,36);        
	textAlign(LEFT);
	text(headlines[index],x,80); 
	x = x - 3;
	float w = textWidth(headlines[index]);
	if (x < -w) {
		x = width; 
		index = (index + 1) % headlines.length;
	}
}

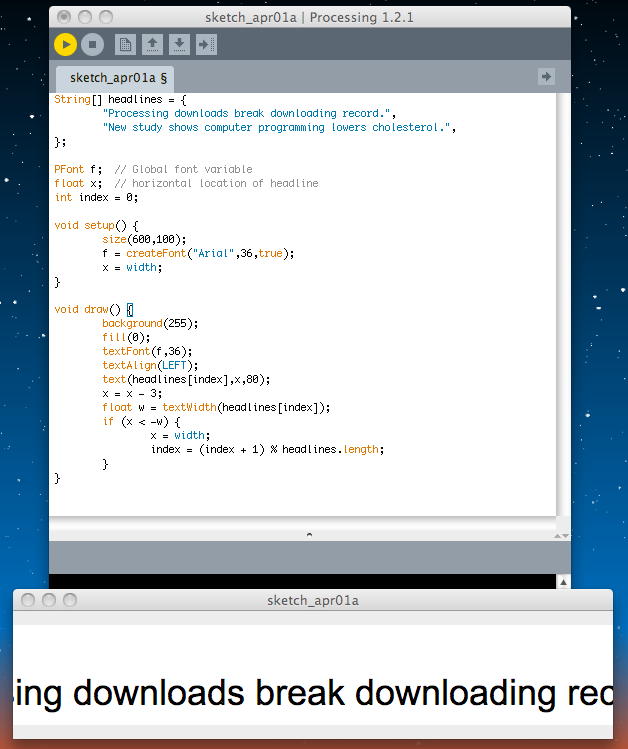
ここでは「textAlign()」と「textWidth()」の例を見たが、Processingではこの他に

• textLeading()
• textMode()
• textSize()

といった文字列ディスプレイ関数も完備しているという。ここでは省略するが、だいたい名前からその機能は想像できる。

次のトピックは「Rotating text」である。まぁJavaベースなので当然と言えば当然だが。このあたりからProcessingらしく面白くなってきそうだ。 回転の「rotate()」は文字列も対象に出来るが、その回転の中心は「translate()」で指定できる。 以下の例では、文字列の中心を回転の中心にしている。 アプレットとして書き出してみると、このようになった。

PFont f;
String message = "this text is spinning";
float theta;

void setup() {
	size(400, 400);
	f = createFont("Arial",48,true);
}

void draw() { 
	background(255);
	fill(0);
	textFont(f);                  // Set the font
	translate(width/2,height/2);  // Translate to the center
	rotate(theta);                // Rotate by theta
	textAlign(CENTER);            
	text(message,0,0);            
	theta += 0.02;                // Increase rotation
}

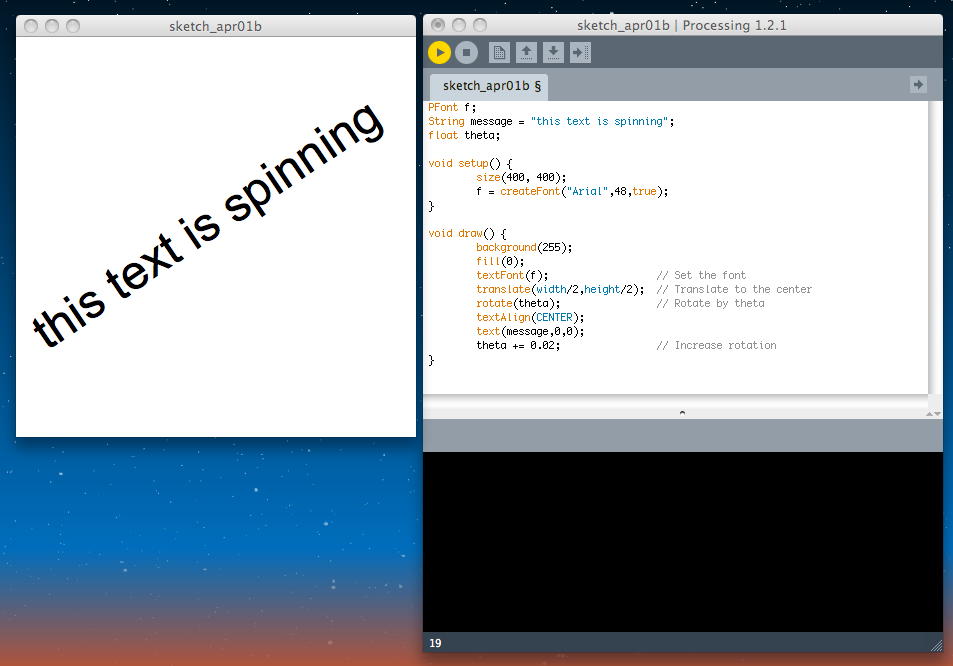
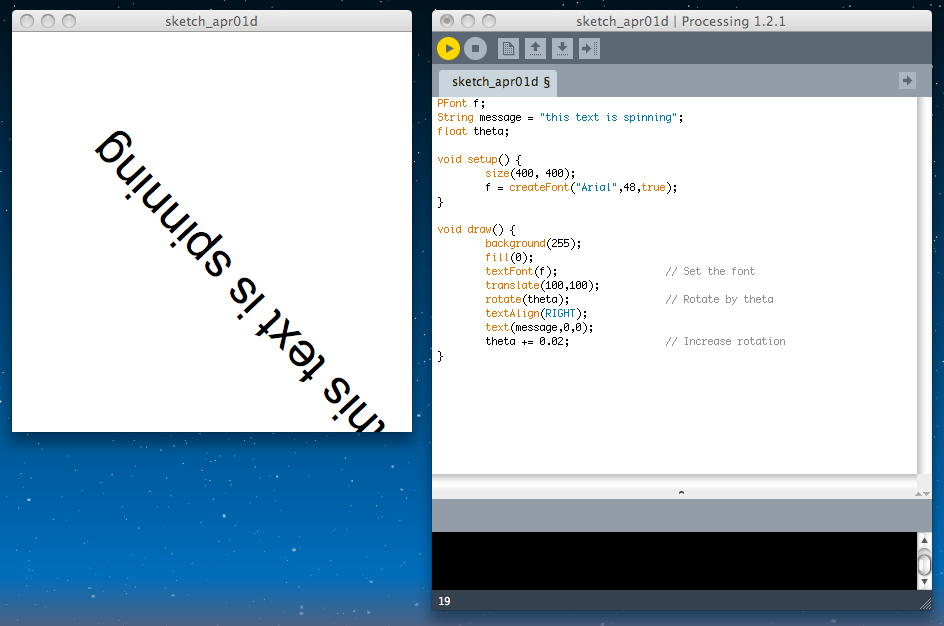
以下の例では、回転の中心位置を変更し、さらに文字列の右端を中心とした回転にしてみた。 アプレットとして書き出してみると、このようになった。

PFont f;
String message = "this text is spinning";
float theta;

void setup() {
	size(400, 400);
	f = createFont("Arial",48,true);
}

void draw() { 
	background(255);
	fill(0);
	textFont(f);                  // Set the font
	translate(100,100);
	rotate(theta);                // Rotate by theta
	textAlign(RIGHT);            
	text(message,0,0);            
	theta += 0.02;                // Increase rotation
}

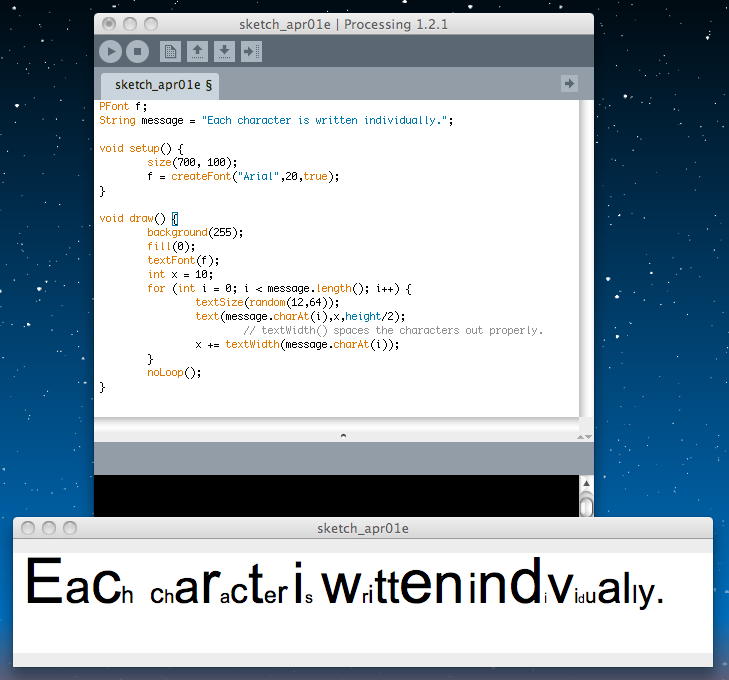
次のトピックは「Displaying text character by character」、つまり文字列が1文字ずつだんだんと出てきたり、1文字ずつ色が付いていくようなアニメーションである。 これは「text("a bunch of letters",0,0);」というような単純な記述では実現できず、文字列を構成する1文字ずつを指定して操作することが必要である。 そこで登場するのが、「charAt()」関数である。 以下の例では、文字列から1文字ずつ取り出して、ランダムな大きさで並べて描画している。 「textWidth()」によって、それぞれの文字の具体的な座標とかを計算していないで詰めてくれるところがポイントだろう。

PFont f;
String message = "Each character is written individually.";

void setup() {
	size(700, 100);
	f = createFont("Arial",20,true);
}

void draw() { 
	background(255);
	fill(0);
	textFont(f);         
	int x = 10;
	for (int i = 0; i < message.length(); i++) {
		textSize(random(12,64));
		text(message.charAt(i),x,height/2);
			// textWidth() spaces the characters out properly.
		x += textWidth(message.charAt(i)); 
	}
	noLoop();
}

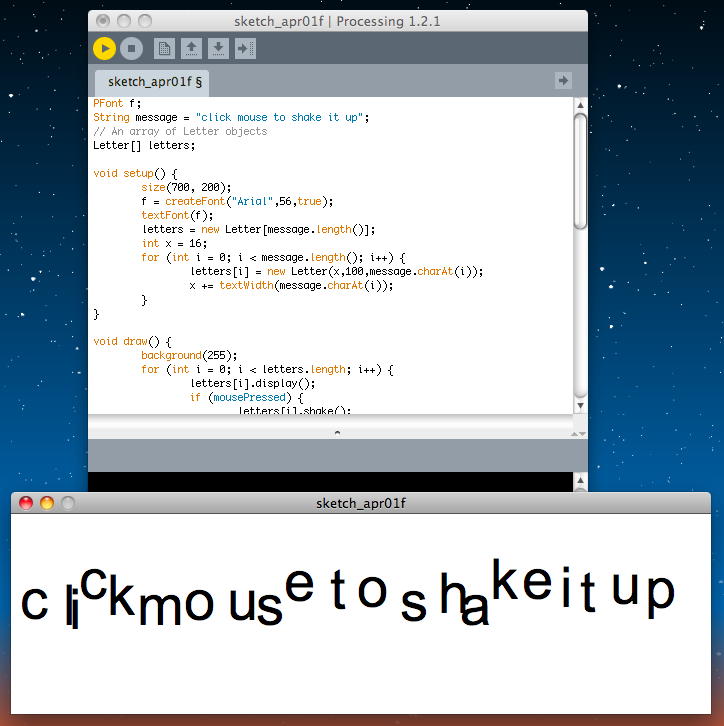
文字列を1文字ずつにバラしてアニメーションさせるには、OOPSであるProcessingのメリットを生かして、親の文字列の持つ性質を子の文字に継承させるのが有効である。 以下の例では、それぞれの文字の初期位置を継承させた上で、マウスをクリックしている間は文字列がバラバラの文字となってそれぞれランダムウォークする。 アプレットとして書き出してみると、このようになった。

PFont f;
String message = "click mouse to shake it up";
// An array of Letter objects
Letter[] letters;

void setup() {
	size(700, 200);
	f = createFont("Arial",56,true);
	textFont(f);
	letters = new Letter[message.length()];
	int x = 16;
	for (int i = 0; i < message.length(); i++) {
		letters[i] = new Letter(x,100,message.charAt(i)); 
		x += textWidth(message.charAt(i));
	}
}

void draw() { 
	background(255);
	for (int i = 0; i < letters.length; i++) {
		letters[i].display();
		if (mousePressed) {
			letters[i].shake();
		} else {
			letters[i].home();
 		}
	}
}

// A class to describe a single Letter
class Letter {
	char letter;
	float homex,homey;
	float x,y;
	Letter (float x_, float y_, char letter_) {
		homex = x = x_;
		homey = y = y_;
		letter = letter_; 
	}
	void display() {
		fill(0);
		textAlign(LEFT);
		text(letter,x,y);
	}
	void shake() {
		x += random(-2,2);
		y += random(-2,2);
	}
	void home() {
		x = homex;
		y = homey; 
	}
}

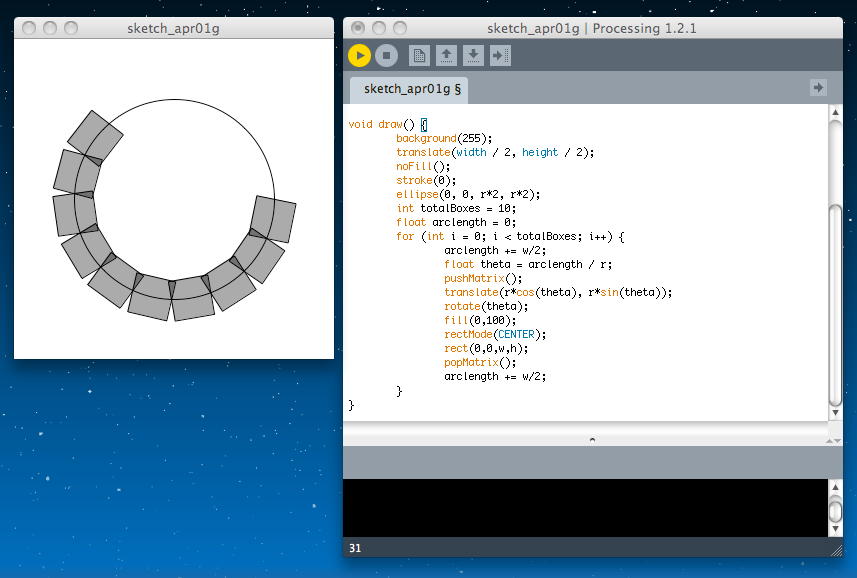
文字列を1文字ずつにバラせれば、「テキストを曲線に沿って表示」というのも出来る。 まず、文字の前に、円周上に矩形を10個並べるというのを試した以下の例では、数学的な幾何計算をたくさん行っている。

PFont f;
float r = 100;
float w = 40;
float h = 40;

void setup() {
	size(320, 320);
	smooth();
}

void draw() {
	background(255);
	translate(width / 2, height / 2);
	noFill();
	stroke(0);
	ellipse(0, 0, r*2, r*2);
	int totalBoxes = 10;
	float arclength = 0;
	for (int i = 0; i < totalBoxes; i++) {
		arclength += w/2;
		float theta = arclength / r;     
		pushMatrix();
		translate(r*cos(theta), r*sin(theta));
		rotate(theta);
 		fill(0,100);
		rectMode(CENTER);
		rect(0,0,w,h);  
		popMatrix();
 		arclength += w/2;
	}
}

文字列でこれを行う場合の相違点は、上の矩形は同じ幅だったが、文字列ではそれぞれの文字によって幅が違うことである。そこで「textWidth()」関数を使って、以下のように文字ごとにその幅を変えて配置すればよい。

String message = "text along a curve";
PFont f;
float r = 100;

void setup() {
	size(320, 320);
	f = createFont("Georgia",40,true);
	textFont(f);
	textAlign(CENTER);
	smooth();
}

void draw() {
	background(255);
	translate(width / 2, height / 2);
	noFill();
	stroke(200);
	ellipse(0, 0, r*2, r*2);
	float arclength = 0;
	for (int i = 0; i < message.length(); i++){
		char currentChar = message.charAt(i);
		float w = textWidth(currentChar);
		arclength += w/2;
		float theta = PI + arclength / r;    
		pushMatrix();
		translate(r*cos(theta), r*sin(theta));
		rotate(theta+PI/2); // rotation is offset by 90 degrees
		fill(0);
		text(currentChar,0,0);
		popMatrix();
		arclength += w/2;
	}
}

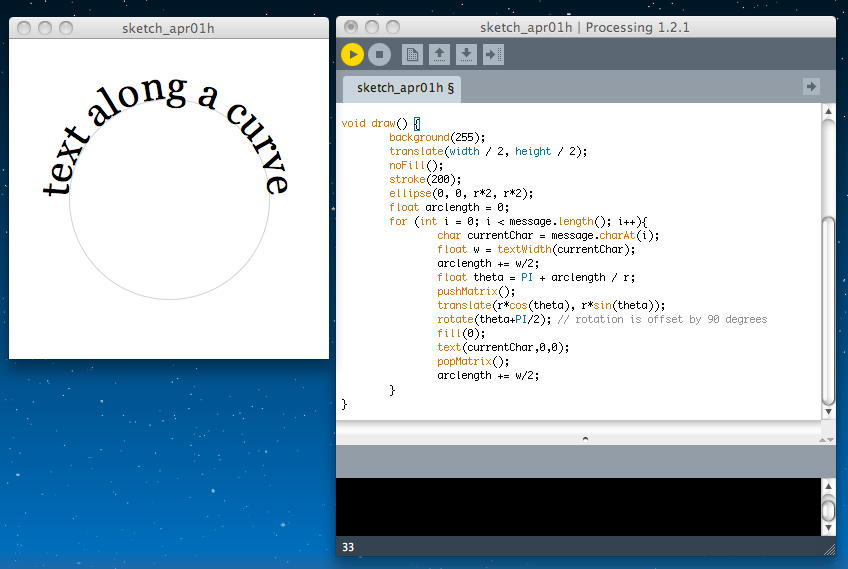
土浦駅に着く直前にここまで来た。これで「Drawing Curves」はおしまいである。

2011年4月2日(土)

日立市で親戚の葬儀に参列したこの日は、本当にごくわずかしか出来なかった。 なんせ、朝7時に土浦駅前のホテルを出て、前夜に借りていたレンタカーでつくばを経由して常磐道を日立まで行き、葬儀のあと逆順でその日のうちに引き返したからである。 以下は東京から浜松までの帰途の新幹線の中で、それもワインをいただきながらの執筆である。(^_^;)

とりあえず、前日は チュートリアル の Drawing Curves までやったので、 2-D Transformations からである。 Processingにビルトインされている「translate」「rotate」「scale」などの変換関数であるが、これは既におおかた登場していたものである。

最初のトピックは「Translation: Moving the Grid」である。 Processingのスクリーンは、以下のように座標軸のある方眼紙、と考えることができ、座標を指定して「rect(20, 20, 40, 40)」などと矩形を描画できる。

この矩形を方眼紙上で移動させるには、以下のように、表示させる座標に移動距離をそれぞれ加算すればよい。

Processingにはこれとは別に、図形をそのままにしておいて、スクリーン、つまり方眼紙の方を移動させて、その結果を表示する、という機能がある。これを「translation」と呼んでいる。

以下の例では、まずグレーでオリジナルの矩形を描画する。 そして次に、矩形を移動して表示させるために座標計算して、赤で描画する。 そして最後に、translateによってスクリーンの方を移動させて、同じ矩形を青で描画する。 両者はスクリーン上で同じ位置となるので、合体してピンクになっている。 ここで、「translate()」を行う前後でpushMatrix()とpopMatrix()とで囲む、という儀式が重要である。 これにより、「元の画面座標」は退避して記憶されていることになる。

void setup()
{
	size(200, 200);
	background(255);
	noStroke();

	// draw the original position in gray
	fill(192);
	rect(20, 20, 40, 40);
  
	// draw a translucent red rectangle by changing the coordinates
	fill(255, 0, 0, 128);
	rect(20 + 60, 20 + 80, 40, 40);
  
	// draw a translucent blue rectangle by translating the grid
	fill(0, 0, 255, 128);
	pushMatrix();
	translate(60, 80);
	rect(20, 20, 40, 40);
	popMatrix();
}

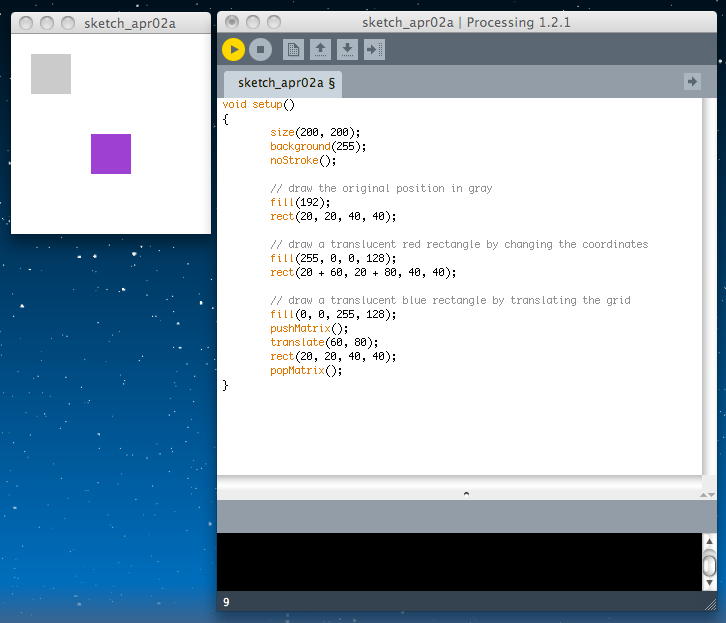
この、スクリーン座標を退避して保管しておくpush/popのメリットを確認するサンプルが以下である。 以下の第一の例は、push/popを使わないプログラミングである。

void setup()
{
	size(400, 100);
	background(255);
	for (int i = 10; i < 350; i = i + 50)
	{
		house(i, 20);
	}
}

void house(int x, int y)
{
	triangle(x + 15, y, x, y + 15, x + 30, y + 15);
	rect(x, y + 15, 30, 30);
	rect(x + 12, y + 30, 10, 15);
}

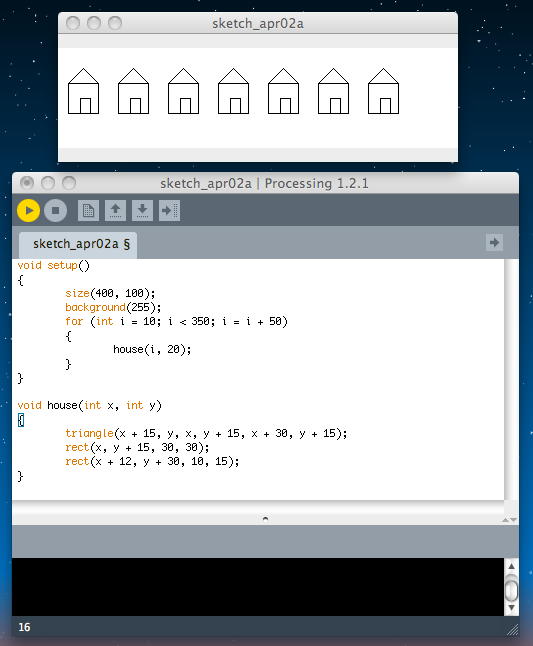
以下の第二の例は、push/popを使ったプログラミングである。 この両者をよく比較して欲しい。 結果はここでは同じである。 そして、コードとしてはこちらの方がpush/popを使っている分だけ、見た目は「より長い」。 しかし、具体的に「家」を描画している部分に、まったく変数が入っていない。 この美しさは、プログラミングにおいては単なる見かけの美しさではない、「清く正しい」美しさなのである。

void setup()
{
	size(400, 100);
	background(255);
	for (int i = 10; i < 350; i = i + 50)
	{
		house(i, 20);
	}
}

void house(int x, int y)
{
	pushMatrix();
	translate(x, y);
	triangle(15, 0, 0, 15, 30, 15);
	rect(0, 15, 30, 30);
	rect(12, 30, 10, 15);
	popMatrix();
}

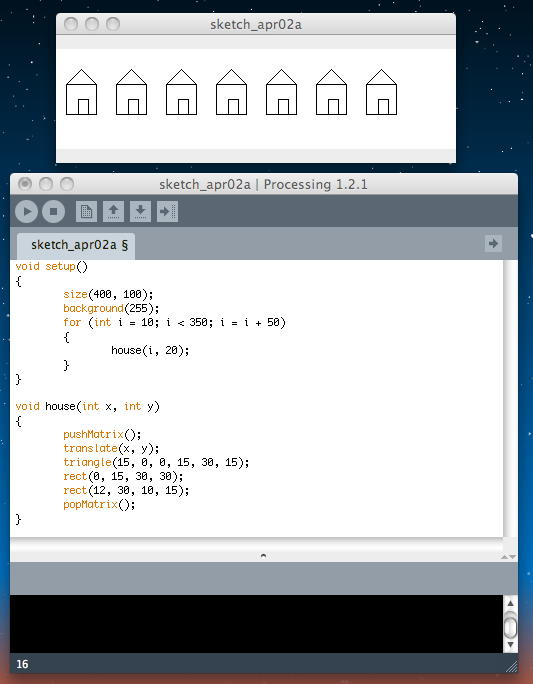
平行移動のtranslationに続いて、rotationである。 回転の単位はラジアンである。 ラジアンと角度の関係は以下である。

ここでも当然、push/popスキームは必須である。 ただし、rotateは回転角度だけでは駄目である。 ある矩形を描画する部分をpush/popで囲んで。その中でこの矩形を45度だけ回転させようとした、以下の例はその間違ったサンプルである。(^_^;)

void setup()
{
	size(200, 200);
	background(255);
	smooth();
	fill(192);
	noStroke();
	rect(40, 40, 40, 40);
  
	pushMatrix();
	rotate(radians(45));
	fill(0);
	rect(40, 40, 40, 40);
	popMatrix();
}

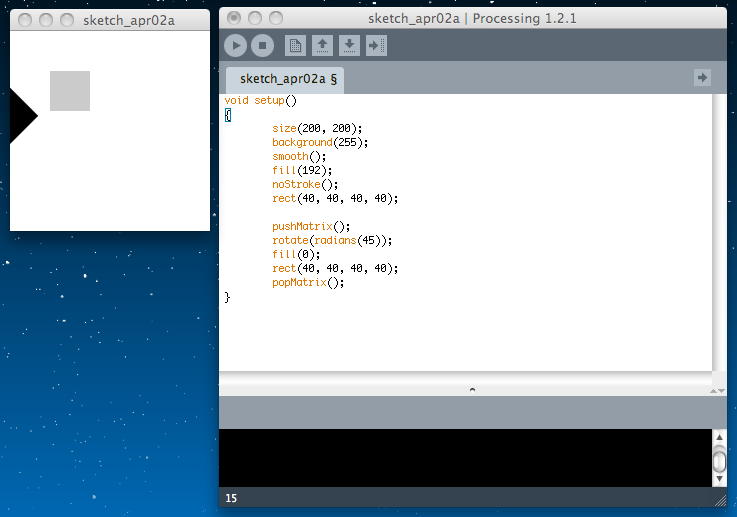
rotateでは、回転角度とともに、その回転の中心が規定されないと、defaultでは以下のように「(0,0)を中心とした回転」となってしまう。

そこで以下のように、push/popの中で、回転「B」の中心もtranslate「A」する必要がある。

以下の例が正しい回転である。 pushして、まず「rotateで回転する中心」を移動させるだけで、あとはpopで元に戻る。

void setup()
{
	size(200, 200);
	background(255);
	smooth();
	fill(192);
	noStroke();
	rect(40, 40, 40, 40);
  
	pushMatrix();
	// move the origin to the pivot point
	translate(40, 40); 
  
	// then pivot the grid
	rotate(radians(45));
  
	// and draw the square at the origin
	fill(0);
	rect(0, 0, 40, 40);
	popMatrix();
}

これを活用した以下の例は、よくある「色のホイール」である。 アプレットとして書き出してみると、このようになった。

void setup() {
	size(200, 200);
	background(255);
	smooth();
	noStroke();
}

void draw(){
	if (frameCount % 10 == 0) 
	{
		fill(frameCount * 3 % 255, frameCount * 5 % 255,
		frameCount * 7 % 255);
		pushMatrix();
		translate(100, 100);
		rotate(radians(frameCount * 2  % 360));
		rect(0, 0, 80, 20);
		popMatrix();
	}
}

次のトピックは、引き続きの「scaling」であるが、ここでもう静岡を過ぎたので、今日はここまで。 明後日は入学式で、いよいよ怒濤の新学期だ。

2011年4月3日(日)

新学期の前日の日曜日、大学は「嵐の前の静けさ」である。 なんとか入学式には、自由創造工房の前の桜も咲いてくれそうだ。

昨日はちょっとだけだが チュートリアル の Drawing Curves の 2-D Transformations を進めたが、その一部のバグをまず追加修正して、次は「Scaling」からである。

「scale()」もまた、push/popで囲んだ中で、座標系を拡大縮小する。以下のように、拡大縮小の基準位置は原点(0,0)である。

void setup()
{
	size(200,200);
	background(255);
  
	stroke(128);
	rect(20, 20, 40, 40);
  
	stroke(0);
	pushMatrix();
	scale(2.0);
	rect(20, 20, 40, 40);
	popMatrix();
}

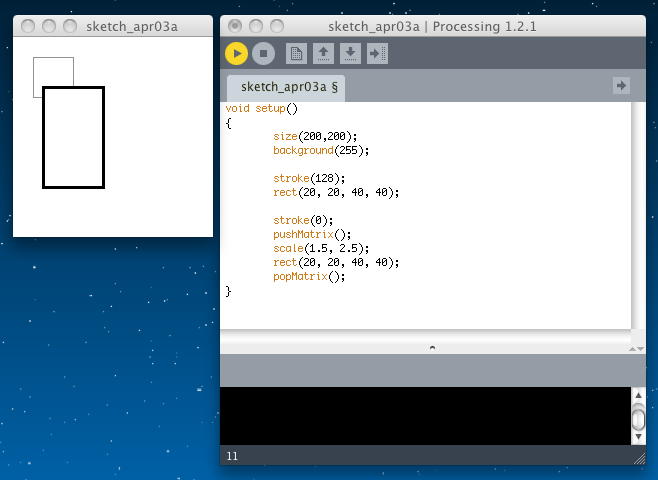
「scale()」の引数が1個であれば単なる拡大・縮小であるが、2個の引数とすると、それぞれx方向、y方向の拡大縮小となる。 以下のようになる。

void setup()
{
	size(200,200);
	background(255);
  
	stroke(128);
	rect(20, 20, 40, 40);
  
	stroke(0);
	pushMatrix();
	scale(1.5, 2.5);
	rect(20, 20, 40, 40);
	popMatrix();
}

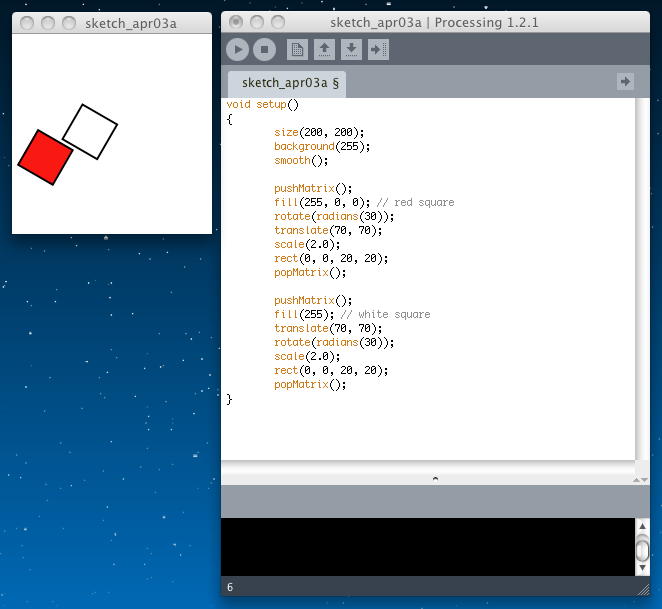
ここで「Order Matters」の注意喚起である。 push/popの中でtranslateやrotateやscaleを行う、その順序が違えば結果も違う、ということである。 以下のサンプルでは、まったく同じパラメータでtranslateとrotateとscaleを行うが、唯一、rotateとtranslateの順番だけ入れかえている。その結果、異なる矩形が描画されている。

void setup()
{
	size(200, 200);
	background(255);
	smooth();
  
	pushMatrix();
	fill(255, 0, 0); // red square
	rotate(radians(30));
	translate(70, 70);
	scale(2.0);
	rect(0, 0, 20, 20);
	popMatrix();

	pushMatrix();
	fill(255); // white square
	translate(70, 70);
	rotate(radians(30));
	scale(2.0);
 	rect(0, 0, 20, 20);
	popMatrix();
}

・・・と、こんなところで今日はオシマイである。 新学期の準備などに追われて、時間があまり無かったので仕方ない。 続きは同じテキストで、いよいよ「3次元の変換」になる。

2011年4月5日(火)

昨日は 入学式 があり、その後は電子制御機器制作室の19台のPCにMax5をインストールして、買い取りiMacの環境設定作業をして、大学院新入生のガイダンスに参加したら、もう終わってしまった。予想通りである。

今日は午後には新入生の学科ガイダンスがあり、その後は履修指導の希望者などが来るので、コマ切れとなっていくが、少しでも進めよう。 チュートリアル の Drawing Curves の 2-D Transformations 「Three-dimensional Transforms」からである。

さきに登場した、「translate()」は、引数が2個であれば、それはxとy方向のスクリーンの移動だったが、これが3つになるとz方向も加わるいう。 また「scale()」は、引数が1個であれば相似的な拡大縮小、引数が2個であればxとy方向それぞれの拡大縮小だったが、これが3つになるとz方向も加わるいう。 また「rotate()」については、引数が1個である「rotateX()」と「rotateY()」と「rotateZ()」という関数があり、それぞれの座標軸に関する回転となって、引数はその回転角度であるという。

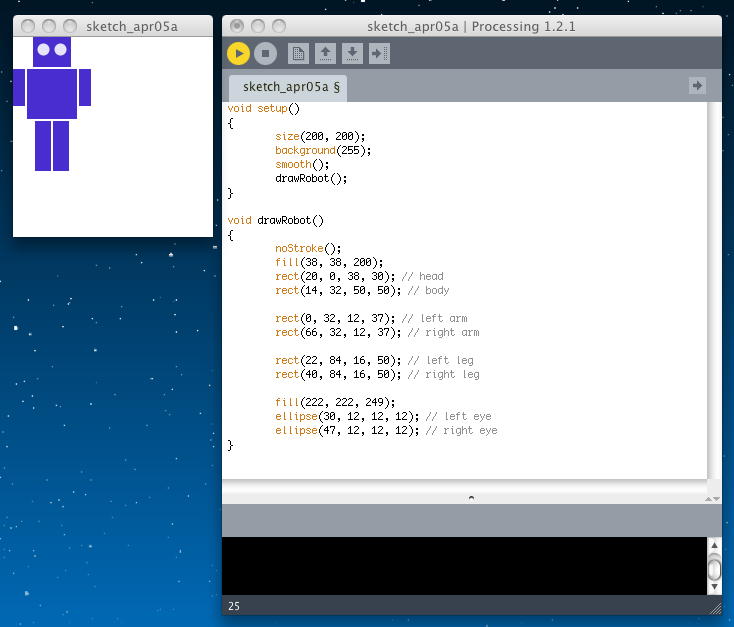
ここで、ケーススタディとして「An Arm-Waving Robot」を取り上げる。 題材となるロボットのデータは、 ここ にある。こんなオープンソースもあるのだった(^_^)。 まずは以下のように、ロボットの概形を簡単に描画する。 身体をパーツに分割しているところがポイントで、後で腕だけ動かすという作戦である。

void setup()
{
	size(200, 200);
	background(255);
	smooth();
	drawRobot();
}

void drawRobot()
{
	noStroke();
	fill(38, 38, 200);
	rect(20, 0, 38, 30); // head
	rect(14, 32, 50, 50); // body

	rect(0, 32, 12, 37); // left arm
	rect(66, 32, 12, 37); // right arm
  
	rect(22, 84, 16, 50); // left leg
	rect(40, 84, 16, 50); // right leg
  
	fill(222, 222, 249);
	ellipse(30, 12, 12, 12); // left eye
	ellipse(47, 12, 12, 12); // right eye
}

次のステップとして、以下の位置にピボット(蝶番)を想定する。ここが腕の回転の中心となる。

そして、以下のように、ロボットの描画において、腕の部分だけを切り離す。 見た目は同じようでも、それぞれの腕のルーチンでは、push/popの中で描画の起点をtranslateしている。

void setup()
{
	size(200, 200);
	background(255);
	smooth();
	drawRobot();
}

void drawRobot()
{
	noStroke();
	fill(38, 38, 200);
	rect(20, 0, 38, 30); // head
	rect(14, 32, 50, 50); // body
	drawLeftArm();
	drawRightArm();
	rect(22, 84, 16, 50); // left leg
	rect(40, 84, 16, 50); // right leg  
	fill(222, 222, 249);
	ellipse(30, 12, 12, 12); // left eye
	ellipse(47, 12, 12, 12);  // right eye
}

void drawLeftArm()
{
	pushMatrix();
	translate(12, 32);
	rect(-12, 0, 12, 37);
	popMatrix();
}

void drawRightArm()
{
	pushMatrix();
	translate(66, 32);
	rect(0, 0, 12, 37);
	popMatrix();
}

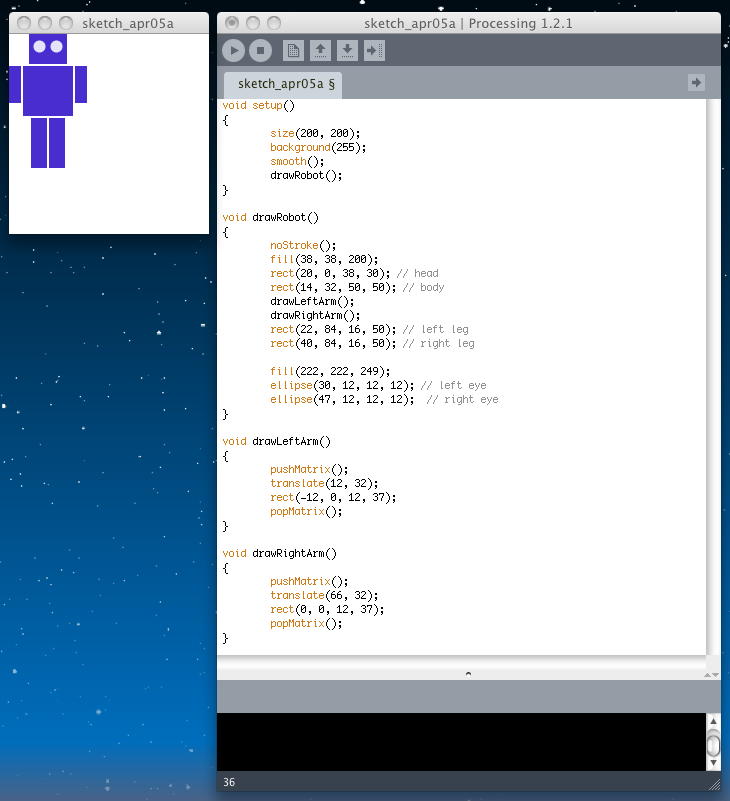
これで道具立てが出来たので、以下のように、腕のルーチンの中で、push/popの中に、さらにrotateを入れてみる。 角度でラジアンを表すためには、「radial()」という便利なものを使う。

void setup()
{
	size(200, 200);
	background(255);
	smooth();
	drawRobot();
}

void drawRobot()
{
	noStroke();
	fill(38, 38, 200);
	rect(20, 0, 38, 30); // head
	rect(14, 32, 50, 50); // body
	drawLeftArm();
	drawRightArm();
	rect(22, 84, 16, 50); // left leg
	rect(40, 84, 16, 50); // right leg 
	fill(222, 222, 249);
	ellipse(30, 12, 12, 12); // left eye
	ellipse(47, 12, 12, 12);  // right eye
}

void drawLeftArm()
{
	pushMatrix();
	translate(12, 32);
	rotate(radians(135));
	rect(-12, 0, 12, 37);
	popMatrix();
}

void drawRightArm()
{
	pushMatrix();
	translate(66, 32);
	rotate(radians(-45));
	rect(0, 0, 12, 37);
	popMatrix();
}

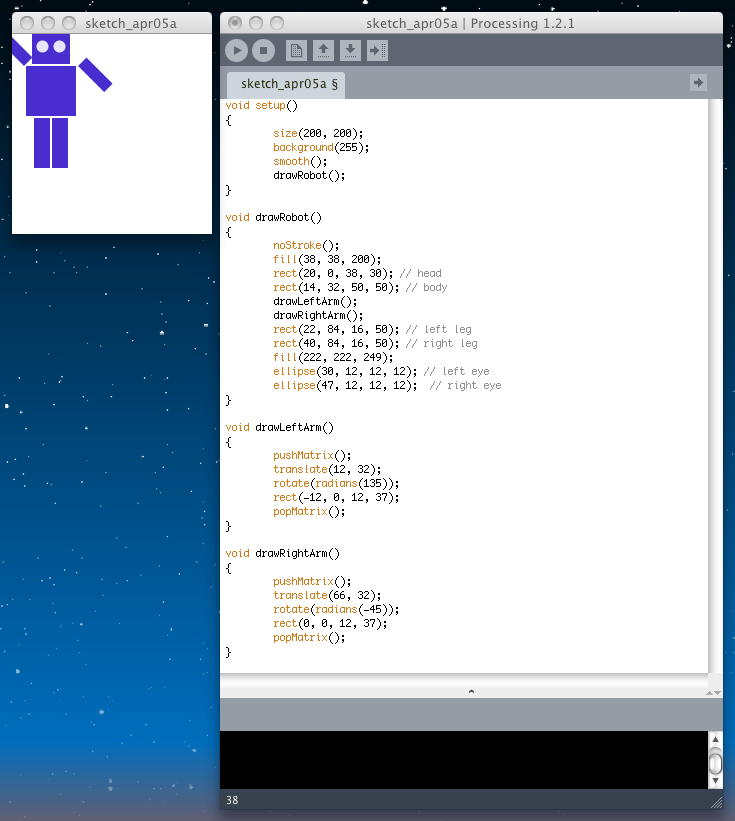
これで準備完了である。あとは、アニメーションとしてそれぞれの腕の回転角度をステップ刻みで変化させ、さらにロボットの全身が画面中央に来るように移動させるだけである。 アプレットとして書き出してみると、このようになった。

int armAngle = 0;
int angleChange = 5;
final int ANGLE_LIMIT = 135;

void setup()
{
	size(200, 200);
	smooth();
	frameRate(30);
}

void draw()
{
	background(255);
	pushMatrix();
	translate(60, 35); // place robot so arms are always on screen
	drawRobot();
	armAngle += angleChange;
  
	// if the arm has moved past its limit,
	// reverse direction and set within limits.
	if (armAngle > ANGLE_LIMIT || armAngle < 0)
	{
		angleChange = -angleChange;
		armAngle += angleChange;
	}
	popMatrix();
}

void drawRobot()
{
	noStroke();
	fill(38, 38, 200);
	rect(20, 0, 38, 30); // head
	rect(14, 32, 50, 50); // body
	drawLeftArm();
	drawRightArm();
	rect(22, 84, 16, 50); // left leg
	rect(40, 84, 16, 50); // right leg  
	fill(222, 222, 249);
	ellipse(30, 12, 12, 12); // left eye
	ellipse(47, 12, 12, 12);  // right eye
}

void drawLeftArm()
{
	pushMatrix();
	translate(12, 32);
	rotate(radians(armAngle));
	rect(-12, 0, 12, 37); // left arm
	popMatrix();
}

void drawRightArm()
{
	pushMatrix();
	translate(66, 32);
	rotate(radians(-armAngle));
	rect(0, 0, 12, 37); // right arm
	popMatrix();
}

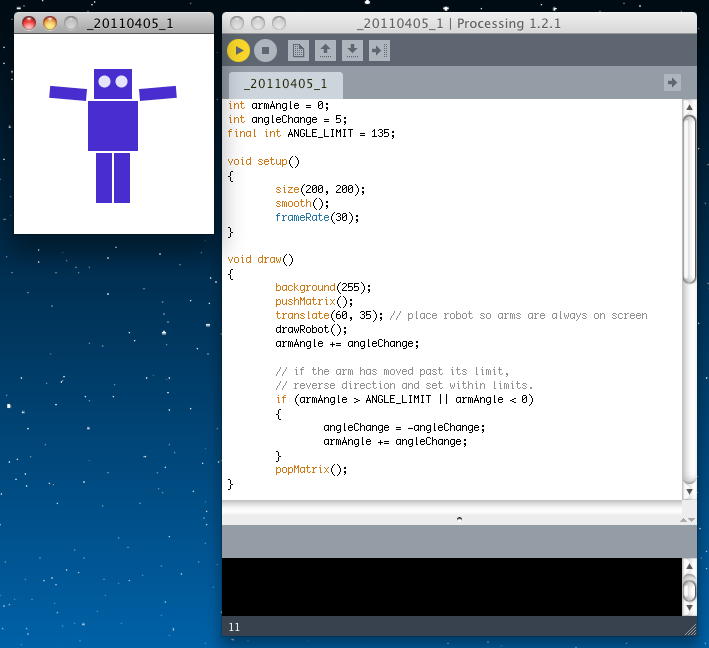
次のケーススタディは「Interactive Rotation」である。 ロボットの腕の角度が時間的に変化するアニメーションに続いて、これをユーザの操作で動かしたい、という事である。 これは今まさに世界中から注目されている、原子炉事故の現場でのロボット作業のリモートコントロールと、本質的には同じことである。 ここでは、マウスのボタンとマウスカーソルの移動で、それぞれの腕を回転させる事を考える。

ロボットには両腕があるが、我々が操作するマウスは、普通は1個である。 過去には以下のように「同時にマウス4個」というシステムも作ったが ★ ★、 これは特別の例外である(^_^;)。 そこで、マウスカーソルがロボットの左側ではロボットの左腕を、反対側ではその逆を操作する、ということにする。

ここで残った問題は、ロボットの腕の回転の中心であるピボット(蝶番)の座標と、マウスカーソルの座標から、具体的にどのような角度で腕を回転させるのか、というところである。 ここで登場するのが「アークタンジェント関数」、「atan2()」である。 この関数は、起点から与えられた点(y,x)までの角度をラジアンで返す。 注意すべきは、y座標が先である点であるが、これはtan関数の逆関数なので仕方ない。 「atan2()」の返す値は、「-π to π radians」つまり「-180° to 180°」である。

「atan2()」の中心が原点ではないので一般化すると、(x0, y0)の点から(x1, y1)の点に回転した時の角度は、 「atan2(y1 - y0, x1 - x0)」 で求められる。 まずは以下の簡単な例で、この新しい関数について馴れておこう。 マウスで矩形をぐりぐりと回転させている。 アプレットとして書き出してみると、このようになった。

void setup()
{
	size(200, 200);
}

void draw()
{
	float angle = atan2(mouseY - 100, mouseX - 100);  
	background(255);
	pushMatrix();
	translate(100, 100);
	rotate(angle);
	rect(0, 0, 50, 10);
	popMatrix();
}

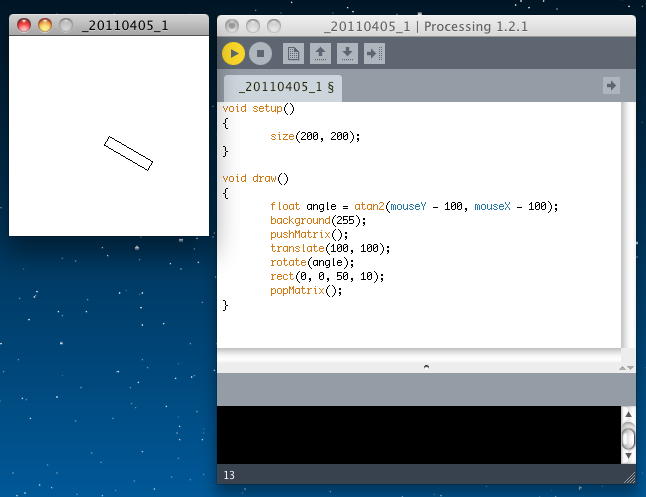
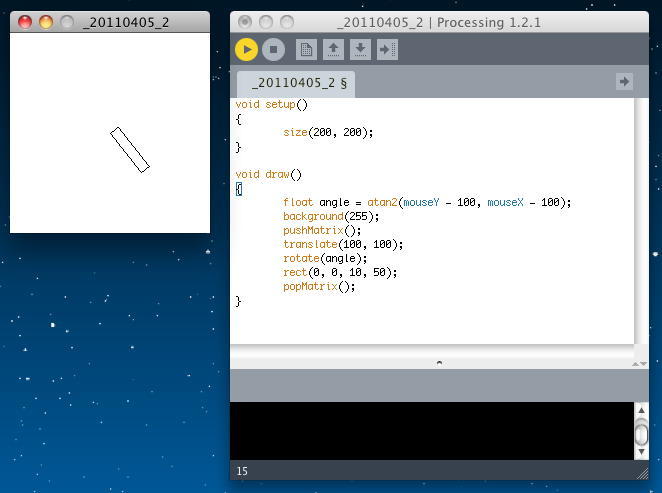
次に、同じプログラムで、描画している矩形のタテヨコだけ、以下のように交換してみよう。 これは正しいプログラムなのだが、人間の目には「マウスに追従」しているようには見えなくなる。 人間の眼は、時計の針のように、「回転の接線方向が短い図形」が回転する、と知覚するからである。 アプレットとして書き出してみると、このようになった。

void setup()
{
	size(200, 200);
}

void draw()
{
	float angle = atan2(mouseY - 100, mouseX - 100);  
	background(255);
	pushMatrix();
	translate(100, 100);
	rotate(angle);
	rect(0, 0, 10, 50);
	popMatrix();
}

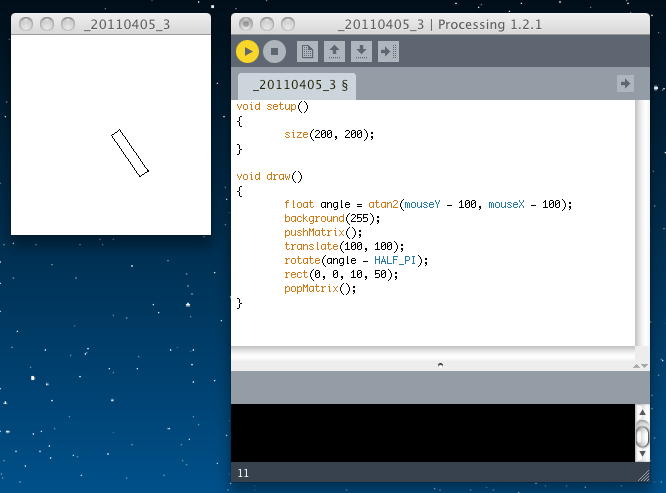
このような場合には、以下のように角度の部分を「(angle - HALF_PI)」とすればよい。 これによって90度だけ回転したことになる。 同様に、「PI (180°)」、「HALF_PI (90°)」、「QUARTER_PI (45°)」、「TWO_PI (360°)」という定数も便利である。 アプレットとして書き出してみると、このように 正しい(人間の目に期待される)動きとなった。

void setup()
{
	size(200, 200);
}

void draw()
{
	float angle = atan2(mouseY - 100, mouseX - 100);  
	background(255);
	pushMatrix();
	translate(100, 100);
	rotate(angle - HALF_PI);
	rect(0, 0, 10, 50);
	popMatrix();
}

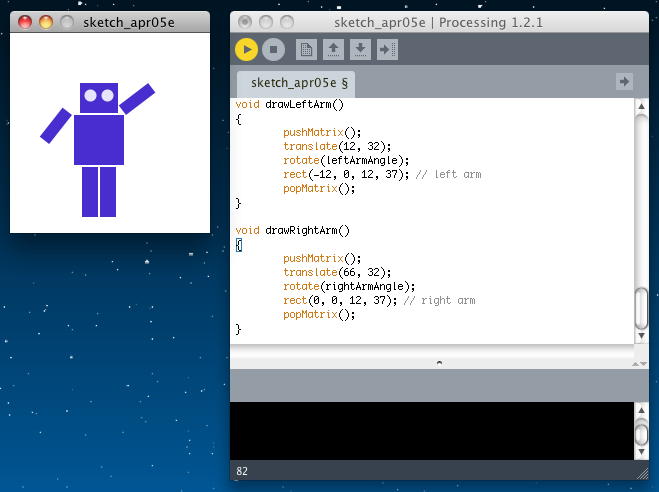
さて、このような準備を経て、いよいよ「マウスでロボットの腕をぐりぐり回転」プログラムである。 以下のようになり、 アプレットとして書き出してみると、このようになった。

final int ROBOT_X = 50;
final int ROBOT_Y = 50;
final int MIDPOINT_X = 39;
final int LEFT_PIVOT_X = 12;
final int RIGHT_PIVOT_X = 66;
final int PIVOT_Y = 32;
float leftArmAngle = 0.0;
float rightArmAngle = 0.0;

void setup()
{
	size(200, 200);
	smooth();
	frameRate(30);
}

void draw()
{
	float mX;
	float mY;
  
	background(255);
	pushMatrix();
	translate(ROBOT_X, ROBOT_Y); 
	if (mousePressed)
	{
		mX = mouseX - ROBOT_X;
		mY = mouseY - ROBOT_Y;
		if (mX < MIDPOINT_X) // left side of robot
		{
			leftArmAngle = atan2
			(
				mY - PIVOT_Y, 
				mX - LEFT_PIVOT_X
			) - HALF_PI;
		}
		else
		{
			rightArmAngle = atan2
			(
				mY - PIVOT_Y,
				mX - RIGHT_PIVOT_X
			)
			- HALF_PI;
		}
	}
  	drawRobot();
	popMatrix();
}

void drawRobot()
{
	noStroke();
	fill(38, 38, 200);
	rect(20, 0, 38, 30); // head
	rect(14, 32, 50, 50); // body
	drawLeftArm();
	drawRightArm();
	rect(22, 84, 16, 50); // left leg
	rect(40, 84, 16, 50); // right leg 
	fill(222, 222, 249);
	ellipse(30, 12, 12, 12); // left eye
	ellipse(47, 12, 12, 12);  // right eye
}

void drawLeftArm()
{
	pushMatrix();
	translate(12, 32);
	rotate(leftArmAngle);
	rect(-12, 0, 12, 37); // left arm
	popMatrix();
}

void drawRightArm()
{
	pushMatrix();
	translate(66, 32);
	rotate(rightArmAngle);
	rect(0, 0, 12, 37); // right arm
	popMatrix();
}

Processing日記(3)

「日記」シリーズ の記録