Electronics Lecture

センサとマイクロエレクトロニクスの概要

1999年3月　長嶋洋一

「電気」の概念と用語

電子回路、と言うと難しいように感じてしまいますが、その基本は

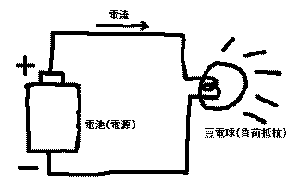
のように、中学校の理科で誰もが体験してきたことです。ここではまず、エネルギー源となる電池があります。電気的にはこのエネルギー源を「電源」と呼びますが、この電源がなければどんな電子回路も動作できない重要な要素です。たとえば停電しても電話ができるのは、電話線から信号だけでなく、電話機本体のための電源が供給されているからなのです。

電源には図のようにプラスとマイナスの極性があり、豆電球を経由して、電源のプラスから一周してマイナスまで戻ってくる「ループ」の構造が必ず必要です。これが「回路」ということで、ここに流れている、と考えるのが「電流」というわけです。実際には電流というのは仮想的な概念であって、その実体はマイナスの電気を帯びた「電子」が、ちょうど電流の向きとは逆方向に流れるということがあとで判明しました。

この図で豆電球に相当するものは、回路の用語では（負荷）抵抗と呼びます。これは、エネルギー源である電源から電流の形で供給された電気的エネルギーを、熱や運動などの別の物理的な形で消費する、という意味になります。日常生活で「電気機器が行う仕事」というのは、結局のところ、この「抵抗」に相当する部分によって、電源から供給されたエネルギーを変換して実現している、ということになります。電気ストーブや冷蔵庫は熱エネルギーに、テレビは電子線を操作して光エネルギーに、ステレオなら音エネルギーに、携帯電話なら通信のための電波のエネルギーに変換されるわけです。

上図を、電子回路らしい記号で書き直したのが、

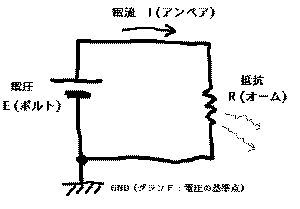
ということになります。中身はまったく同等ですが、ここでは電源の「電圧」としてＥ(ボルト)、電流としてＩ(アンペア)、抵抗としてＲ(オーム)という、それぞれを簡単な数式として扱うための標準的な記号と、単位(いずれもこの分野で発見した科学者の名前に由来します)を定義しています。この回路の原理としてよく「たとえ話」に出てくるものに、電源をダムに見立てて電圧をその水圧として、電流は水流の強さ、抵抗はダムの発電機による水流への抵抗、という説明があります。これは電圧がダムの水の位置エネルギーに相当して、発電機の負荷抵抗によって外部へのエネルギーに変換されると、水としては位置エネルギーを失って戻ってくる、という視点からも確認できます。

上図ではこれらの3要素とともに、電源のマイナス端子の部分に、「GND」(グランド)の記号を記してあります。これは、次に登場するオームの法則など、回路のいろいろな場所の電圧や電流を考える場合の基準点、という意味があります。回路の動作としてはループ状の部分を流れる電流が主役ですから、各地点の電圧を表現するための基準はどこにとっても構いません。たとえば

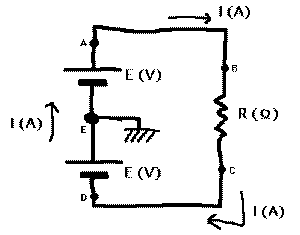
の場合、二つの電源の間にGNDを設定しているために、回路の中には「マイナス」も登場します。この図の場合、回路のどこでも流れている電流はＩアンペアで共通で、回路の各部分の電圧をGND を基準にして、A点とB点はプラスＥボルト、C点とD点はマイナスＥボルト、E点はGNDなのでゼロボルト、などと扱うことになります。これをその地点の「電位」といいます。

「素子」：いろいろな登場人物

ここまでを整理すると、電子回路とは「電流の流れるループ」によって成立する、ということになります。そしてこのループの構成要素としては「電源」「抵抗」を紹介しました。また回路図では、線で結んだあらゆる地点の電圧が同じである、という事が前提になります。たとえば上図であれば、A点からB点までを結んでいる電線はどんなに長く描いても関係なく、いわば「ゼロ抵抗」ということです。また、回路図の中に複数のGND記号があった場合、それらも理想的なゼロ抵抗で全て接続されている、ということになります。

ここでは他の登場人物として、次に紹介する各種の半導体素子（能動素子と言います）を除く、「受動素子」について整理しておきましょう。

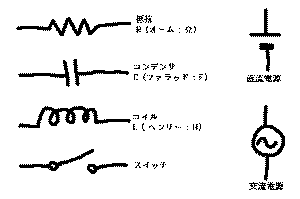
は基本的な受動素子や基本的な回路要素を並べたもので、既に抵抗と直流電源については触れています。また、いくつか新しい記号と単位が登場してややこしくなってきますが、我慢して下さい。今後、それほど種類が増えるものでもありません。

回路を構成する受動素子として抵抗と並ぶものはあと二つだけです。その一つは「コンデンサ（静電容量）」というもので、抵抗値をよくＲ(Registance)の記号で表すのと同じように、Ｃ(Capacitance)の記号で表します。単位は、抵抗の「オーム」（Ω）に対して「ファラッド」（Ｆ）となります。その実体は図のように、向き合った電極が離れている構造をしています。ということは、電流が流れていってくれませんから、一見するとまったく無意味に思えるのですが、実はこれは直流の場合の話です。コンデンサは直流回路では、いわば「無限大の抵抗」というものですが、回路に交流の電流が流れる場合には、後述するような重要な特性によって、いわば「交流回路の主役」となります。

もう一つは「コイル（インダクタ）」というもので、図のようにグルグル巻きの電線のような構造をしているものです。記号ではＬ（InductanceなのでIとしたかったが、電流がIなのでLとした）、単位は「ヘンリー」（Ｈ）です。これも図から考えると、巻いていても結局は電線であれば、抵抗ゼロで何も関係ないように思われます。事実、理想的な直流回路ではその通りなのですが、これが交流回路になると、重要な役割を果たすのです。なお、理科の実験で使われる「電磁石」とは、このコイルに鉄心を入れて磁力を強化したものです。つまり、コイルとは「電気的エネルギーと磁気的エネルギーの変換器」という側面もあることに注意しておきましょう。

その下の「スイッチ」は、見た通りのものでそれほど重要なものではありません。直流回路では、ONとなってゼロ抵抗で電流を流す電線となり、OFFなら無限大の抵抗として回路のループを切り離してしまう、というだけのことです。また、電池の記号で直流電源を表すのに対して、交流電源（周期的に電流の向きや大きさが変化し続ける電源）の記号もあわせて紹介しました。具体的な内容については、このあとで詳しく検討します。

「オームの法則」：奥が深い基本中の基本法則

ですが、複雑な電子回路においても、あらゆるところでオームの法則が出現している、という事はあまり意識されていないようです。

オームの法則は、いろいろな角度から眺めてみることができる、非常に重要な基本法則なのです。たとえば、この式は自然界でもっとも重要な「線型性」の表現として、

　「回路を流れる電流は、電源の電圧に比例する」---(1)

という定義から来ています。つまり、「抵抗Ｒの逆数」をこの比例関係の「比例定数」として、

　「回路の抵抗は、その両端の電圧に比例し、流れる電流に反比例する」---(2)

と定義していることになります。すると、この単純な式を色々に眺めることで、

　「ある抵抗の両端の電圧は、そこを流れる電流に比例する」---(3)

　「電流が共通の回路中の抵抗の両端の電圧は、その抵抗値に比例する」---(4)

などという性質も出てきます。さらに、

　「同じ電圧の与えられた回路を流れる電流は、その回路中の抵抗値に反比例する」---(5)

ということも、ＩとＥとＲの記号を変換するだけで導くことができます。そして、より複雑な回路や次の「交流回路」を考える時に重要になるのが、オームの法則の基本的な性質として、

　「回路のどこをとっても必ず成立する」---(6)

　「どの瞬間であっても必ず成立する」---(7)

ということが言える、という点です。（厳密に言えば、交流で電圧と電流の「位相」が異なる場合には成立しないのですが、ここでは簡単のために同位相として考えます）

オームの法則を具体的に適用する事例として、「合成抵抗の公式」は覚える必要がない、オームの法則でいつでも得られる、という事を確認してみましょう。

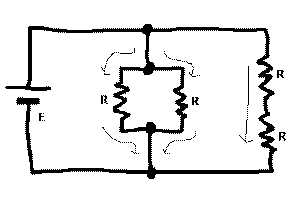
上図には4個の抵抗が書かれていますが、これをさきほどの図と比較して、「抵抗の合成公式」をオームの法則で考えてみよう、というわけです。

さきほどの図に書かれたＥ、Ｒ、Ｉと、この上図とは全て同じものと考えてみましょう。すると、抵抗が1本の場合には、電流Ｉが流れることになります。ところで、上図の中央の、並列接続された2本の抵抗Ｒの部分にそれぞれオームの法則を適用すると、左右それぞれのルートに電流Ｉが流れていることになります。そこで、この「並列接続された等しい2本の抵抗」を「合成された1本の抵抗」と考えると、同じ電圧で2倍の電流を流すことから、抵抗値は半分である、ということになります。また、上図の右側の、直列接続された2 本の抵抗Ｒの部分にそれぞれオームの法則を適用すると、流れる電流はともに等しいのでこれをI'とすると、上下それぞれの抵抗の両端の電圧は「I'×Ｒ」で、この和がＥになることから、I'はＩの半分であることが導かれます。つまり、半分の電流が流れているということは、「直列接続された等しい2本の抵抗」はそれぞれの抵抗値の2倍である、ということになります。

このように、回路図のどこにでもオームの法則を利用できる事を知っておくのは重要なことなのです。たとえば

の中央の2本の抵抗の部分は、電源の電圧Ｅを抵抗R1と抵抗 R2とで「分圧」している、という回路です。このそれぞれの抵抗のところにオームの法則を適用してみると、V1の地点の電位（GNDとの間の電圧）は、電源の電圧Ｅをこの2本の抵抗値に比例した割合で分割していることが簡単に導けます。これを利用したのがこの図の右側のボリューム（可変抵抗器、記号はＶＲ）で、V2の地点の電位は、電源電圧ＥからGNDのゼロボルトまで、連続的に変化させることができるのです。ステレオのボリュームで音量を変化させているのは交流の信号ですが、交流でもオームの法則は成立しますから、音量が簡単に制御できるわけです。

直流と交流

さて、ここで「電源」の種類を整理しておくと、

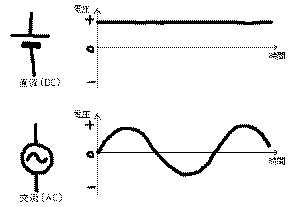
のように、「直流電源」(DC)と「交流電源」(AC)とがあります。 ACでは時間とともに電圧の大きさも極性も変化していますから、ここに抵抗が接続されていれば、瞬間ごとにオームの法則を適用すると、電流も同様に変化していることが判ります。ただし、コンデンサとコイルでは、事態はより複雑になります（後述）。

ところで、実際に電子回路で電源として使われるのは全て直流で、交流はコンセントから供給される形態、というのが一般的です。この理由は、電子回路というのは本質的に「変化しない安定な直流の電源において動作する」ように設計されているものだからです。それでは電力会社から直流でコンセントに来ればいいのに、と思いますが、交流には「トランスという部品によって、高いエネルギー効率で任意の電圧に変換できる」という特性があるために、この部分はどうしても交流が必要になります。つまり、発電所から超高圧の電圧で交流送電し、変電所、電柱の上の変圧器（トランス）を経て家庭の100Vコンセントにエネルギーを供給する、ということは、直流のままでは無理なのです。

また、回路の中のいろいろな場所の電圧というのは、もちろん理想的な直流ということではありません。

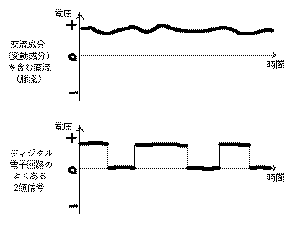
の上図ように、変動成分（交流成分とも呼びます）を持っていて極性としては変わらない「脈流」が代表的なものであり、さらに電子回路の主役となるディジタル回路では、下図のように、GNDレベルと一定電圧レベルとを瞬間的に行き来するような電圧が、回路のどこでもほとんど見られます。このようなディジタル信号というのは、なめらかな交流信号よりも急激な変化の連続（それも、たいていの場合にはとても高速）であるために、そのまま各種の「ノイズ発生源」ともなりうるものだ、ということを頭に置いておきましょう。

電力とエネルギーの考え方

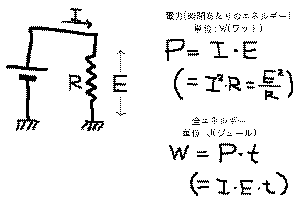
はいつもの基本回路で、抵抗Ｒの両端にＥの電圧がかかり、この時にＩの電流が流れている、という直流的な定常状態にあるものとします。ここで「電力」は電圧と電流の積、と定義され、さらにここにこの電力が消費され続けた時間ｔを掛けたものがエネルギー、と定義されます。つまり「電力」とは「単位時間(1秒)あたりのエネルギー」というような量なのです。

受動素子の特性と加算法則

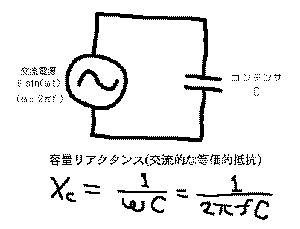
のコンデンサと、

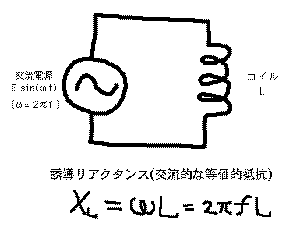
のコイルについてペアで整理すると、とても簡単になります。

図のように、交流電源としては、一般にサイン関数で表現される「正弦波」が使われます。周期的に変化する交流波形であれば、全て複数の正弦波の合成によって表現できる、という事実（フーリエ分解／フーリエ合成）がありますから、ここではこの式として一般性は失いません。ここで「ω」という量は、毎秒あたりの「繰り返し回数」である周波数「ｆ」（単位はヘルツ：Ｈｚ）に「２π」という定数を掛け算した量です。また、周波数の逆数は「1周期に要する時間」という量で、「周期」（単位は秒）になります。

すると、静電容量がＣ（Ｆ）であるコンデンサが交流回路で等価的に抵抗として働く抵抗値である「容量リアクタンス」（記号はＸC、単位はΩ）は、図のように「１／ωＣ」と簡単な式で表現されます。言い換えれば、まったく直流を通さないコンデンサも、交流回路ではこの式に従った一種の抵抗、として働くことになります。直流の周波数はいわばゼロHz（変化しない）ですから、確かにこの式では抵抗成分が無限大になります。また、同じＣの値に対して、

　「ＸCは周波数が高いほど交流的抵抗成分が小さくなる」

という点を確認しておきましょう。

同様に、コイルの図では、インダクタンスＬ（Ｈ）であるコイルが交流回路で等価的に抵抗として働く抵抗値である「誘導リアクタンス」（記号はＸL、単位はΩ）は、図のように「ωＬ」と簡単な式で表現されます。言い換えれば、直流では理想的には抵抗ゼロであるコイルも、交流回路ではこの式に従った一種の抵抗、として働くことになります。直流の周波数はいわばゼロHz（変化しない）ですから、確かにこの式は直流でも成立しています。同じＬの値に対して、

　「ＸLは周波数が高いほど交流的抵抗成分が大きくなる」

という点を確認しておきましょう。これは、コンデンサとコイルが、まったく逆の性質を持っていることを意味しています。

電磁気学の教科書では、ここで「電荷」という量を登場させて、何故、電気的に切れている筈のコンデンサが交流を「流す」のか、という説明があるところですが、この点は省略します。また、何故、抵抗ゼロの電線を巻いただけのコイルが交流では抵抗となるのか、については、中学の理科で学んだ「電磁誘導」から説明できるのですが、これも省略します。興味のある方は調べてみるといいでしょう。

さて、抵抗の直列接続／並列接続の公式と同じように、コンデンサにもこういう公式があります。ここでは「電荷」という概念を省略しているので、結果だけ紹介すると、

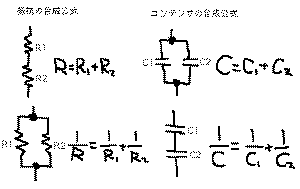
のようになっています。これは「抵抗とは逆」ということですから、覚えるのは簡単でしょう。また、「コイルの合成」というのは、実はこれまた省略している「自己誘導」「相互誘導」という概念が必要になるので、ここでは省略しておくことにします。実際の場面では、コイルよりもコンデンサの方が圧倒的に登場する（コイルの合成を計算することはほとんど無い）ので、実用上はあまり問題はありません。

インピーダンス

ここまでに登場した、抵抗、コンデンサ、コイルという主要な受動素子が、電子回路においては単独でなく組み合わされた形で、さらに交流特性をもって動作する、というのが実際的な回路技術の基本となります。そこで最後に登場する基本用語が「インピーダンス」というものです。これは、既に紹介した単独の抵抗やコンデンサやコイルの交流的な抵抗成分でなく、これらが組み合わされた場合の合成抵抗のようなものです。交流回路においては、現実には回路中の電圧と電流は時間的に同じように変化するわけではないために（これを「位相がずれている」と言う）、単純にそれぞれの抵抗成分を加算することはできないのです。

また、現実の電子回路では、これまでゼロ抵抗であるとしてきた電線やプリント基板の銅箔面やGNDも、高い周波数では等価的に抵抗成分やコイル的な成分が無視できなくなってきます。そこで、理想的には抵抗ゼロ、コンデンサやコイル単体と考えてきたところに、実効的な抵抗成分を合成したインピーダンスを考える必要があるのです。いったんインピーダンスとしてまとめてしまえば、あとは既に述べたように、このインピーダンスを「抵抗」と見なして、エネルギーなどを検討できるわけですから、このインピーダンスの公式は、最後のステップというわけです。

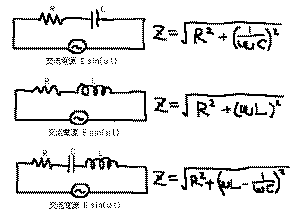
が、代表的なインピーダンスの公式です。これを複素数やベクトルで数学的に導出することは、興味のある人への課題としておきますが、結果だけメモしておけば、とりあえず設計の場には十分なのです。なお、インピーダンスの記号は一般にＺで、単位は抵抗と同じΩ です。抵抗Ｒの逆数は「電流の流しやすさ」ということになるのですが、同様に考えたインピーダンスの逆数のことを「コンダクタンス」と言い、単位はなんとΩ記号を上下にひっくり返して「モー」（ohmの逆なのでmho）と呼びます。(^_^;)

微分回路と積分回路からフィルタへ

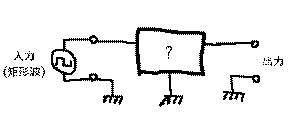
のような回路を考えます。ここでは入力として正弦波の交流でなく、一般的なディジタル回路の信号である、電源電圧（+5Vが多い）とGNDとを交互に行き来する、図のような「矩形波」（上下の時間がそれぞれ 50%である波形をこう呼ぶ）であるとしましょう。そして、入力の矩形波が図のブラックボックスの動作によってどう変化するか、という視点で考えてみましょう。ところで、このブラックボックスに使う部品は、まずは簡単のために抵抗とコンデンサの二つだけ、ということにします。これは、コンデンサとコイルとは互いに反対の性質なので、必要な交流的動作は一方だけでも実現できるためです。また、コンデンサは小型の電子機器に搭載できるような小型化が進んでいますが、コイルはサイズが大きくなるためです。さて、

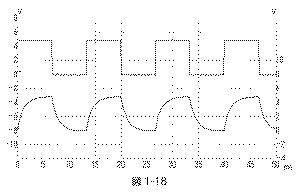
は、筆者が実際に電子回路を「ブレッドボード」という実験器具を使って組み立てた回路で、オシロスコープという計測装置によって記録した、「生のデータ」です。細かい変動（一種のノイズ）が乗っていることからも判るように、現実の電子回路の信号とは、このように理想的な信号とは大きく異なっています。図の見方ですが、二つの信号波形のうち上段は全て共通で、これは図1-15の左側の入力信号です。電圧のメモリはグラフの左側になりますから、ほぼ「GND」と「+5V」を行き来している矩形波信号であることが判ります。また下段は、それぞれの回路の出力信号であり、電圧のメモリは右側で読みます。図1-19のように、入力はプラスの範囲の電圧でも出力にマイナス電圧が現れることもあります。

さて、これら4種類のオシロスコープ波形から、それぞれの電子回路をパッと当てられる人は、もうプロの領域です。正解は

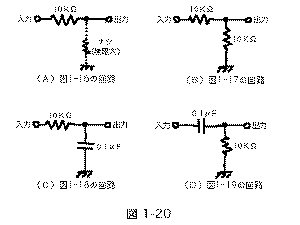
のようになります。図の（Ａ）は入力から10KΩの抵抗を経てそのまま出力に出ているだけ、というものです。ここで入力と出力については、信号点だけを記号で明示して、それぞれの電圧の基準点であるGNDの部分は省略して描かない、という一般的ルールにも注意しておきましょう。抵抗を経由しているのに入力と出力の電圧がまったく同じなのは不思議だ、という人は、点線で描いてある、GNDとの間の無限大の抵抗と10Kオームとで入力を「分圧」している、と考えてみれば、納得がいくと思います。

図の(B)は、入力から出力に10KΩの抵抗があり、さらに出力とGNDの間にも10KΩの抵抗がある、というものです。これは入力の電圧が半分に分圧されている回路、という事ができますが、確かに図1-17の電圧をよく見てみると、そうなっています。ここまでは抵抗だけなので、まったく直流回路と同じ考え方でいけます。

図の(C)は、入力から出力に10KΩの抵抗があり、さらに出力とGNDの間には0.1μFのコンデンサを入れた回路です。これは入力の電圧が分圧されているうち、一方がコンデンサに置き換えられたもの、という見方ができます。ところで既に述べたように、コンデンサとは交流的な成分に対しては通過させてしまう、という性質があります。もう少し細かく言えば、「高い周波数成分ほど通しやすい」「急激な変化分ほど通しやすい」ということです。

図1-18 をこの性質を頭に置いて眺めてみると、回路の入力電圧がGNDから +5Vに、あるいは逆に+5VからGNDに急激に変化した点では、出力はなめらかに変化しながら目標地点になめらかに漸近していることが判ります。これは、急激な変化成分ほどコンデンサによってGNDに流れて(捨てられて)、出力信号の成分としてはカットされている、という意味になります。図 1-20(C)のような位置のコンデンサは、いわば「変動成分を吸収する緩衝装置(バッファ)」「交流成分をGNDにバイパスさせる」というような機能があります。前者を強調して、この回路を「平滑回路」と呼びますし、後者の機能を称した「パスコン(バイパスコンデンサ)」という部品名があるくらいです。

図1-20 の(D)はこれとはちょうど反対に、入力から出力に 0.1μFのコンデンサがあり、さらに出力とGNDの間には 10KΩの抵抗を入れた回路です。この場合、入力の電圧が分圧されている一方がコンデンサに置き換えられたもの、と見てみると、周波数の高い、つまり急激な変動成分ほど出力に現れることになり、極端には「定常的」な成分は直流ですから、コンデンサによってカットされて出力がゼロになっていく事を意味します。また、入力信号が上昇する時と下降する時とでは、抵抗を流れる電流の向きが逆方向になるために、出力にはGND電位をはさんで、プラスとマイナスの両方の電圧(交流)が生じる、ということになります。

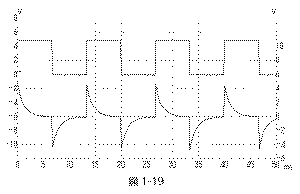
この定性的な視点から図1-19 を眺めてみると、入力信号の電圧がGNDから+5Vに瞬間的に上昇する、という急激な変化点(時間ゼロなら理論的には無限大の周波数)では、最大値として電源電圧と同じプラスの電圧となりますが、その次の瞬間には入力は+5Vで定常的となるので、出力電圧はゼロに向かって漸近していきます。入力が+5VからGNDに変化する時にはこの逆となり、出力にはマイナス方向に反転したような信号が現れて、これもゼロに向かって漸近していきます。この回路はいわば、入力の変化点だけに反応する出力が得られるもので、「エッジ検出回路」とも言います。

さて、ここで重要な回路が2つ、登場してきました。これらは多くの場面で非常に重要な意味をもつので、さらに検討しておくことにしましょう。

図1-20 の(C)の回路は「積分回路」とも呼ばれていますが、これは「電位差に比例した電流が流れる」という条件のもとに、入力信号を時間軸方向に積分すると、まさに出力信号が得られることによります。ここでは詳しい数学的な扱いについては省略しますが、コンデンサの「電荷」の概念を定義すると、簡単な微分方程式の例題となります。そして重要なのは、

のように、抵抗の代わりにコイルを用いることで、信号の周波数に対する特性はより強化されるために、図のような入出力特性を持った「低域通過型」と呼ばれるフィルタ(ローパスフィルタ：ＬＰＦ)を構成できるという点です。これは、たとえば信号線に必要な信号以外の高域の不要信号が乗っている場合、LPFによってこの成分だけを大幅に減衰させることができる、という作用があることになります。

また同様に図1-20 の(D)の回路は「微分回路」と呼ばれています。これも、時間的に遅延を持った条件の元で入力信号を時間で微分した出力が得られるためです。これを

のように抵抗をコイルで置換すると、下図のように、今度は「高域通過型」のフィルタ(ハイパスフィルタ：ＨＰＦ)となります。これは、たとえば信号線に必要な信号以外の低域の不要信号が乗っている場合、LPFによってこの成分だけを大幅に減衰させることができる、という作用があることになります。極端な例としては、信号として交流を扱っている回路に不要な直流電流が乗っている場合、この回路のコンデンサだけで(コイルや抵抗を取り去る)、直流はカットされて問題を解決できることになります。ただし、必要な交流信号の周波数帯域が広い場合には、小さなコンデンサは低域でのインピーダンスが大きくて減衰してしまいますから、十分に大きな静電容量のコンデンサを必要とします。

「能動素子」：電子回路の基本要素

そして何より、「増幅」作用という、受動素子には絶対に真似できない特性があります。増幅というのはその名の通り、入力の信号幅よりも大きな信号幅の出力を得る、というものです。日本語となっている「アンプ」とは、この増幅(Amplify)から来ているものです。そして、増幅作用を持つ能動素子により、発振、スイッチング、演算、通信、センシング、制御、などのあらゆるエレクトロニクス動作が可能となります。能動素子こそ、電子回路の主役です。

ここで取り上げるのは、以下の種類のものです。これだけの種類を大体でも理解していれば、エレクトロニクス技術のほとんどの領域で困ることはないでしょう。

　・交流から直流を得るために必要な「ダイオード」

　・増幅などあらゆる動作の基本要素の「トランジスタ」

　・多数のトランジスタを集積したICの「OPアンプ」

　・多種多様なファミリからなる「ディジタルIC」

　・能動素子だけでなく一部受動素子もある「光素子」

　・自然界の物理量を電気的情報に変換する「センサ」

　・ハードウェアとソフトウェアの統合した「マイコン」

また、能動素子そのものではありませんが、関連してとても重要となる「電源と電池」についても検討します。

ダイオード回路

は、そのもっとも基本となるダイオードの動作を示したもので、ダイオードＤは、記号の中の三角の頂点の向きにのみ電流を流し、逆方向ではちょうどスイッチを切ったように、非常に大きな抵抗となって電流を流さない、という機能があります。これは、このような「極性」のなかった受動素子との大きな違いで、この性質から色々な電子回路が実現できるのです。本書では、このような半導体の性質の原理である「p型半導体」「n型半導体」「PN接合」というような話を省略して、こういう性質の素子なのだ、ということで進めていくことにします。

この「一方通行でのみ電流を流す」というダイオードの性質を活用した電子回路の例としては、AMラジオで受信した電波の信号から音声信号を得るための「検波回路」、そしてあらゆる電子機器の電源に必須の「整流回路」などの例があります。実は名前は違いますが、検波回路も整流回路も、本質的にまったく同じダイオードの性質を利用しています。

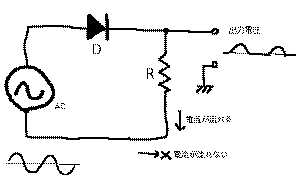
のように、直流電源でなく交流電源がダイオードに与えられた回路を考えてみると、実はこれは検波回路では周波数が相当に高いという違いがあるだけで、この整流回路と動作原理はまったく同じです。検波回路の場合には、図の出力電圧を音声信号として利用しますし、電源の整流回路の場合には、図の抵抗Ｒの部分が、電源を必要としている負荷回路（電子機器の本体の部分）となります。なお電源回路では、このあとに「出力をより直流に近づける」ための「平滑回路」が入りますが、実はこれは既に紹介した積分回路（ローパスフィルタ）そのものです。

ダイオードにはこのような一般的なもの、後述する発光ダイオードの他に、逆電圧（電流が流れない向きにダイオードにかかっている電圧）の大きさに応じて、等価的なコンデンサ（直流電流を流さないのでコンデンサと見なせる）の静電容量の大きさを変化させることのできる「バリキャップ」（可変容量ダイオード）などというものもあります。また、

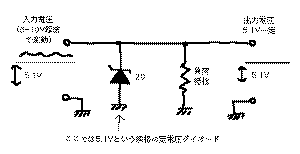
の「ツェナダイオード」（定電圧ダイオード）は電子回路において重要なもので、規格ごとに一定の基準電圧があり、これを超える逆電圧については突然にダイオードとしての整流作用を失ってONになってしまうため、両端の電圧として得られる出力電圧が一定の電圧になる、一種の定電圧電源として利用できます。実際の定電圧電源回路では、ある程度以上の電流を取り出すためにトランジスタと組み合わせるものの、基準となる定電圧発生部分にはツェナダイオードが使われています。

トランジスタ回路

のように型式の付け方は、「高周波用」「低周波用」という組み合わせから4種類に区分けされています。トランジスタの型番を見て「2SD***だからNPN型で、ここは低周波回路だな」などと判ることも時には重要な知識となります。ただし、高周波タイプといっても具体的な周波数の定義はなく、さらに「大は小を兼ねる」というのか、高周波タイプのトランジスタで低周波回路を組んでもまったく問題ないために、決めつけることはできないので注意しましょう。

トランジスタ回路の全ての基本は、

のような「増幅回路」です。増幅というのは、「入力の変化よりも大きな出力の変化（電圧や電力）を得る」というもので、電源のエネルギーを入力信号の小さな変化に対応させて変化させる機能、と位置づけることができます。

は、さきの回路の入力電圧（左側の縦軸）と出力電圧（右側の縦軸）とを実際の回路により計測した例です。上段の入力電圧は、 0.15V程度の振幅であるのに対して、下段の出力振幅は1.2V 程度にまで増幅されていることがわかります。なお、この図では入力電圧が細かく振動しているのに出力にあまり反映されていませんが、これは入力電圧を計測していたオシロスコープの部分でノイズを拾っている（実際の信号にはこの成分はあまり乗っていない）、ということも判ります。またこの回路では、入力信号と出力信号の極性が反対になっている、つまり「反転増幅器」であることにも注意しておきましょう。

さて、このようなトランジスタの基本的な増幅回路から始まって、実際的な電子回路というのは非常に多くの種類があります。たとえば

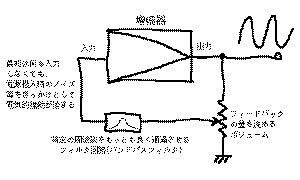
の「発振回路」では、普通の増幅回路の出力の一部を入力にフィードパックさせてやります。その際、途中に特定の周波数帯域をもっともよく通すようなフィルタ回路を入れておくと、出力のうちこの周波数の成分が再び増幅されて出力に出る、という動作を繰り返すことで、この周波数成分の信号を連続的に発生する、という回路が構成できるわけです。また、

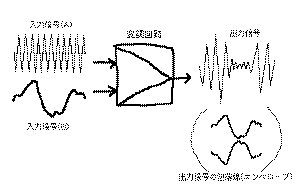
の「変調回路」とは、入力に2種類の信号を与えて1つの出力信号を発生する回路です。この例では、入力Ａとして高い周波数で一定振幅の信号と、入力Ｂとして別の信号を与えた結果として、出力信号はＡの周波数でＢの振幅変化を持つものとなります。これは、普通に聞いているAMラジオの信号そのものであり、振幅変調と呼ばれているものです。変調とは見方を変えれば、2種類の信号を1本に多重化している、という働きであり、多くの電子回路でこの応用回路を見ることができます。

トランジスタの応用回路でアナログの世界からディジタルへと移行する上で重要なのが、「スイッチング回路」です。たとえば、

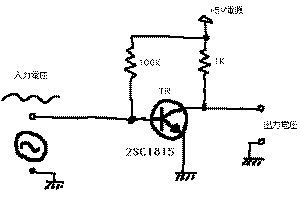
は、さきの増幅回路とも似ている増幅回路ですが、ベース端子のところの抵抗の入れ方（バイアスといいますが、本書では深入りしません）によって、出力電圧はほぼ電源電圧フルスケールとGNDとをスイングするようになります。

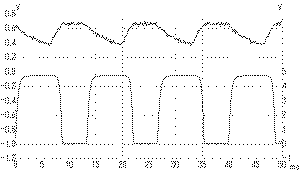
はこの回路で実際に測定した信号で、入力電圧（左側の縦軸）と出力電圧（右側の縦軸）とを比べてみると、これも反転増幅器ですが、信号の形は大きく歪んでいます。これがオーディオアンプであれば、原音とは似ても似つかないヘンに音になりますが、ディジタル電子回路では、このように「飽和した回路」を使うのが一般的です。つまり、入力のアナログ的な信号は、この回路によって「１」(+5V) か「０」(GND)という、ディジタルの明確な値になっているというわけです。この場合、上段の入力信号のような小さなノイズは下段の出力信号では完全に無視されていることから判るように、ディジタル回路とは、基本的に小さなノイズには強い、という性質を持っています。

トランジスタの一種であるFET(電界効果トランジスタ)は、トランジスタが電流増幅（原理的には入力電流の変化が出力電流の変化となる）のに対して、電圧増幅（入力電圧で出力電流を制御する）を行う素子として、多くの電子回路で利用されています。FETには3端子と4端子、PチャンネルとNチャンネル、MOS型と接合型、など非常に多くのタイプがあり、端子の名称も「ソース」「ドレイン」「ゲート」などと変わりますが、ここでは紹介のみに止めます。

OPアンプ回路

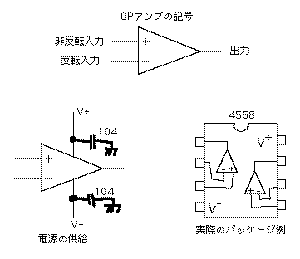
のように単純な2入力のアンプであり、実際には多数のトランジスタによる高性能な増幅回路をブラックボックスの単純な「部品」として提供しているものです。図のように、8ピンのパッケージに2回路分のOPアンプ、あるいは14ピンで4回路入っているタイプも多く使われています。OPアンプは増幅度がとても高い「理想アンプ」なので、図のように2つの電源端子に対して、パッケージのすぐ近くに「パスコン」と呼ぶコンデンサを取り付けます。

OPアンプには、多くの種類の応用回路があります。簡単に基本回路とともに紹介しておくと、

の反転増幅回路、

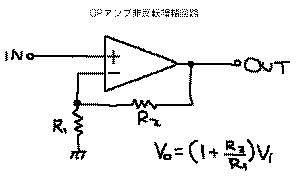
の非反転増幅回路、加算回路や減算回路を実現できる

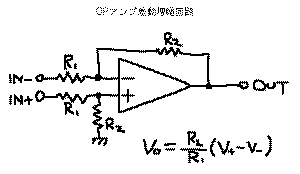
の差動増幅回路、ゲインが1倍で入力インピーダンスが非常に大きいためにバッファによく使われる、

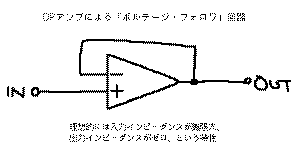
の「ボルテージ・フォロワ」回路、

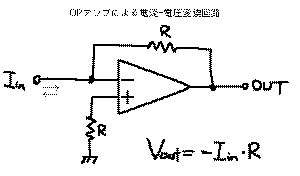
の「電流－電圧変換回路」、

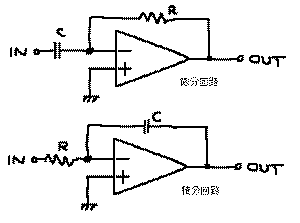
の微分回路と積分回路、などがあります。また、OPアンプのゲイン（増幅度）が非常に大きいことを利用して、入力電圧の差を無限大まで増幅することで入力の大小に対して出力が正負の電源電圧のいずれかになる、というコンパレータ（比較器）回路もよく使われます。

ディジタルIC回路

ディジタルICのもっとも基本的な単位となるのは、

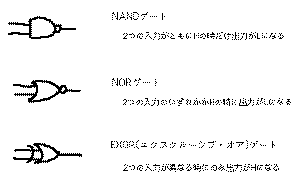
のような「ゲート」と呼ばれる基本的な論理回路です。実際のICでは、

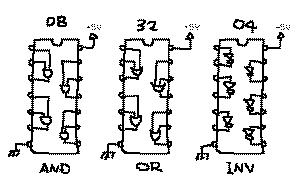
のように、14ピンのパッケージに同じゲートが4つずつ入っているものが一般的です。このようなディジタルICファミリのパッケージでは、電源ピンとGNDピンの場所が決まっていますので、知らない回路でも電源とGNDラインを追いかけることは容易にできます。

ディジタル回路では、基本的にはこれらのゲートを組み合わせて任意のシステムとしていくのですが、よく用いられる機能ブロックは、それぞれがICとして提供されているために、本当にゲートで回路を組むのはごく一部でいいようになっています。このような機能ブロックICとしては、入力ディジタル情報の組み合わせによって出力信号が選ばれる「デコーダ」、入力データを2進数情報として加算する「加算器」（アダー）、複数の入力から指定されたものを選択して出力する「マルチプレクサ」などがあります。これらはいずれも、入力が与えられるとほぼ同時に出力が現れる（厳密には回路の遅延がある）もので、「論理回路」と分類されています。

この論理回路に対して、もう一つの重要なディジタル回路のグループが「順序回路」、あるいは「同期回路」と呼ばれる一群です。このもっとも基本的な要素は、

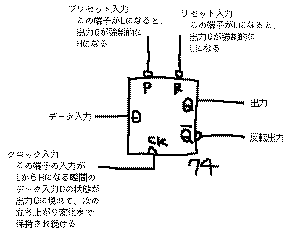
のフリップフロップという回路です。かなり複雑に見えますが、プリセットとリセットは主に初期設定のための補助端子と見ると、入力はデータDとクロックCK、そして出力はQという単純な構造になります。そして、入力Dが出力Qに現れるのはクロックCKがLからHに変化する「立ち上がりエッジ」と呼ばれる変化点であり、他の時にはこの内部状態が保持されている、というところが論理回路と決定的に異なるところです。つまり、フリップフロップとはもっともシンプルな記憶回路（メモリ）であり、CKが変化しなければデータは絶対に変化しない、というものです。

この順序回路の特性を、さらに大きな機能ブロックICである「カウンタ」によって検証してみましょう。

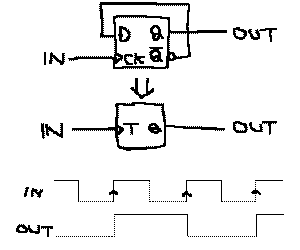
は、先のフリップフロップ（これをDフリップフロップとも呼びます）の反転出力を入力Ｄに与えて、全体として「クロックCK端子を入力、出力端子Qを出力」として動作するブロックの回路で、この全体を図のように「Tフリップフロップ」とも言います。この動作を端子の信号の定義から追いかけてみると、図のように入力クロックの立ち上がりエッジごとに出力が反転することになります。これは、入力と出力の周波数で言えば「半分の周波数に変換する」ということであり、この回路は「分周回路」とも呼ばれます。

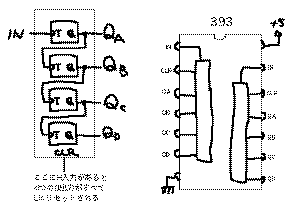
の左側は、このTフリップフロップの出力を次段の入力として次々に与えて4段構成としたブロックで、右側はこの4段ブロックが1つのICパッケージにまるまる2個入った、 393というポピュラなディジタルICの内部構成図（回路図）です。ちっぽけなICの中に、何百ものトランジスタからなる回路が入っているのですが、このICを使う場合には、端子として定義されるディジタルの状態だけを考えればいい、まさにブラックボックスとなっています。

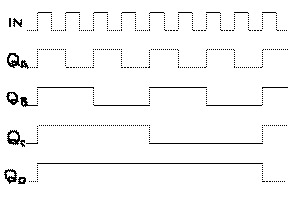
はこの4段のフリップフロップの部分の信号の動作を表したものですが、入力クロックに対してそれぞれの段の出力は「2のn乗分の1」という関係の周波数となります。

ディジタル回路技術としてこの他にどうしても必要となる知識としては、

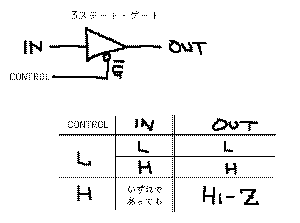
の「スリーステート・バス」があります。ここまではディジタル回路の信号は「H(+5V)」と「L(GND)」の2種類しか登場しませんでしたが、実はもう一つ、「ハイ・インピーダンス状態（トライステート状態とかスリーステート状態などとも呼ぶ）」というものがあり、実際的なマイクロコンピュータシステムなどには欠かせないものなのです。3ステート出力（もともとH、L、とハイインピーダンス状態の3種類から来ている）が可能なのは通常のゲートとは異なる専用のゲートに限られ、図のように制御入力によって通常のディジタル出力かハイインピーダンスかを選択し、通常状態であれば入力の信号がそのまま出力される、というものです。

この図だけを見ていても、3ステートゲートの機能についてはピンと来にくいでしょう。これは、

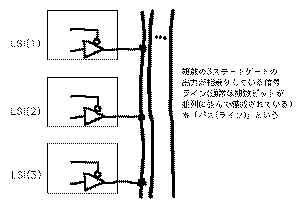
のように、複数の3ステートゲートが信号を乗せる「バス」と呼ばれる信号ラインとともに意味を持ってくるのです。たとえばマイコン回路では、中心となるマイクロプロセッサ(CPU)のデータ信号ラインはデータバスといって、ここにメモリや周辺 LSIが接続されています。それぞれのビットの信号線には CPUを含むそれぞれのLSIの3ステート出力ゲートが接続されていますから、「同時に2つ以上のゲートが出力される」という状態（ゲートの素子破壊にもつながる）は絶対に起こらない（排他的に出力が許可される）ように回路動作が設計されています。

さて、この3ステート状態を実際の回路で計測してみましょう。実験回路としては

のように、3ステートゲートの入力として周期的なクロック信号を与えて、これを分周した信号を出力制御端子（Gバー、と呼びます）に与えます。すると下図のように、出力が許可されているLの期間は出力信号としてH－Lと変化することが期待されます。一方、出力が禁止されているHの期間については、このバスラインに信号を乗せるゲートがここでは他にありませんから、「ハイ・インピーダンスで浮いている」と呼ばれる状態になります。これを検証するために、出力信号ラインには、ずっと筆者の指を当てておくことにします。+5Vの電圧ですから別に感電の心配もありません。

は、74HC393と74HC245というICで実際に上の回路を組んで実験した測定データです。上段は3ステートゲートの制御入力、下段は出力の3ステートバスの信号です。確かに、出力イネーブルの期間にはきちんと+5VとGNDの電圧が出力されていますが、出力がハイインピーダンスとなる「不許可」の期間には、触れている筆者の身体に乗っている「ハム」というノイズ（AC電源が人体に誘導して乗る）によって、信号とは言えない状態になっているのがよく判ります。なお、この図を見て「出力に現れるHとLが反対の順序になっていておかしい」と気付いた人はスルドイです。実は簡単のために省略していましたが、393というICのTフリップフロップのCK入力には、信号反転のインバータが入っているために、CK入力信号の立ち上がりエッジでなく、逆の「立ち下がりエッジ」で状態が反転するので、この実験のような出力になるのです。しかし一般には立ち上がりエッジがほとんどなので、前述の説明では混乱を避けるために省略していました。

さて、ディジタルICの中でどうしても紹介しておかなければならないのが、アナログとディジタルの接点となる「D/A 変換回路」や「A/D変換回路」を1チップに専用化したICの一群です。たとえば、連続して変化するアナログ電圧をディジタルデータとするには、

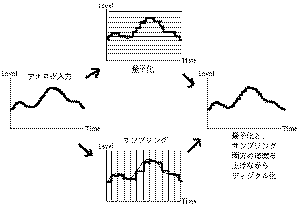
のようにデータの大きさの軸について離散化する「量子化」と、時間軸の方向に離散化する「サンプリング」の二つの側面があります。

実際にディジタルからアナログに変換する回路の動作の実例として、

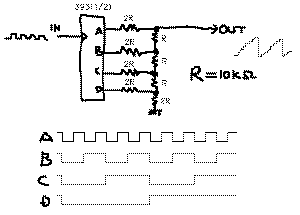
のような回路について調べてみましょう。これは74HC393という4ビットのカウンタの出力が、2進数としてゼロから15まで一つずつ増えていく「インクリメント動作」をすることを利用して、その出力を「ラダー型」という図のような抵抗の接続によってD/A変換して「のこぎり波」の出力を発生する、という回路です。実際にこの回路を組んでオシロスコープで計測したのが

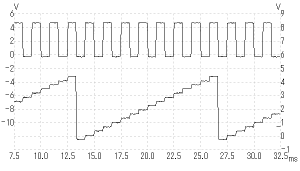
で、ここでは上段は入力のうちもっとも周波数の高いＡの部分、下段がD/A変換の出力となっています。実際に、1チップのD/Aコンバータの内部に、ほぼこのままの回路が入っているICも実際にあるのです。

光素子回路

エレクトロニクスの世界では「光」には大きく二つの重要な性質があります。一つは誰にも明らかな「視覚的媒体」（ディスプレイ）としての利用で、暗闇にたった一つの小さな赤いLEDが点滅するだけで、人間は注意力を喚起される強力なメッセージ能力を持っています。これには

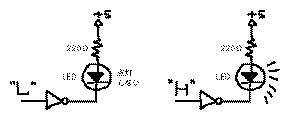
のように、LEDとたった1個の「電流制限抵抗」があれば十分です。人間の五感の中では視覚の情報量が非常に多いので、光素子はこれからも重要な働きをしていくことでしょう。

そしてもう一つ、工場などノイズ環境の劣悪な場所を中心として、気付かれないところで活躍する「光」の性質とは、「電磁気的なノイズの影響が無い」というものです。

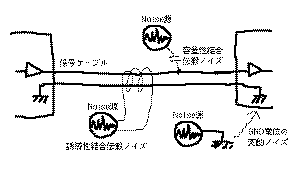
はこの様子を示したもので、必要な信号をケーブルを介して伝えなければならない経路上では、いろいろなノイズ源からの電磁気的な影響が加わります。これに対して、

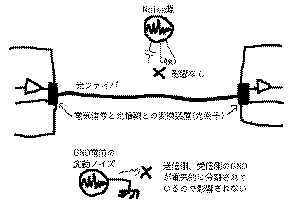
のように機器間に光ファイバケーブルを使った場合には、電磁気的なノイズは相互作用の起こしようがないために、まったくノイズの影響はありません。さらに光によって両者のシステムのGNDが電気的に分離できるために、GND 電位の変動、というノイズに対しても強力になります。

光ファイバを用いるほどの本格的対応でなくても、

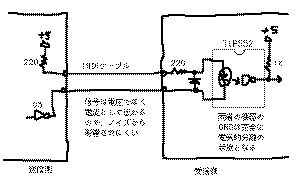
の「フォトカプラ」という光素子を用いると電気的に回路を分離できるために、耐ノイズを大きく向上することができます。この例は、世界中のメーカの電子楽器を相互に接続できるMIDIという国際標準規格のインターフェース回路で、フォトカプラによって送信側と受信側の電源もGNDも完全に分離しているために、一方の機器の漏電や故障が他方に及ばないようになっています。また製造機器や制御機器などでは、大電力のリレーをON/OFFさせる部分にフォトカプラを用いて電気的に分離し、リレーの接点から発生するノイズが電子回路に影響を与えるのを抑えるようになっているのが一般的です。

センサ回路

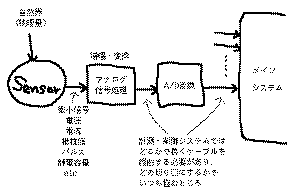
のように、電子機器は基本的に外界の物理量をセンサによって電気的信号に変換し、さらにこの微弱信号を増幅したり変換した電気信号をいくつものセンサから集めて処理していきます。

「センサ回路」というのは、心臓部のセンサそのものと、アナログ信号処理を行う電子回路とから構成されますが、物理量を電気信号に変換するセンサ自体は単純なものがほとんどです。たとえば「曲げセンサ」というのは、荷重で抵抗値が変化する「歪みゲージ」という抵抗素子であり、「加速度センサ」についても、その実体は加速度によって変形するバネの変形量をこのゲージで検出しています。湿度センサやジャイロ(角速度)センサも、結局のところは抵抗値としてセンサ出力が得られます。そして、この信号を伝達可能な大きさに増幅するアナログ回路というのは、既に紹介したOPアンプによる色々な信号変換回路です。

マイコン回路

スーパーコンピュータからパソコンまで、あらゆるコンピュータは基本的に全て、このCPUが中心になっていますが、外見としてコンピュータが見えないものも、現代の電子機器のほとんどが実はマイコンを搭載しています。たとえば自動車には数十個のマイコンがあって、あるCPUはエンジン制御、あるCPUはブレーキ制御、と多数で共同してシステムを構成しています。また、ビデオやエアコンの本体の制御はもちろん、それぞれのリモコンにも実は小型のマイコンが入っているのです。パソコンにしても、本体の中枢部に強力なCPUがあるだけでなく、キーボード内に一つ、ハードディスク内にも一つ、と多数のマイコンがそれぞれの部分の制御をしながら、全体として情報交換してシステムを構成しています。携帯電話も「たまごっち」も、列車内の電光掲示パネルも、全てそれぞれの中にマイコンがあって実現しているシステムなのです。

世の中にCPUは何百種類とあるのですが、マイコン回路としての本質的な部分では、全て同じような構成をしています。

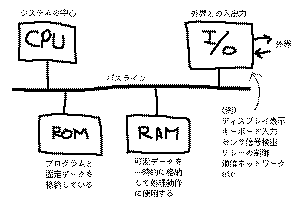
のように、構成要素としては、中心となる「CPU」、プログラムや固定データなどを格納する「ROM」 (読み出し専用メモリ)、データ等を一時的に格納して読み書きする「RAM」、そして外界との入出力のやりとりを総称した「I/O」というブロックです。パソコンなど一部のコンピュータでは、プログラムの大部分をRAMに置いて色々に変更できるようにしていますが、各種の電子機器に組み込まれているマイコン回路は、ほとんど全てがこの構成です。

本当は、この図の「バス」には

　・データが相乗りする「データ・バス」

　・メモリのアドレスを指定する「アドレス・バス」

　・読み書きの制御などの信号の「コントロール・バス」

に分かれているのですが、ここでは深入りを避けます。また、アドレス信号からメモリや複数のI/Oを排他的に選択してバスの使用権を与えるために「アドレス・デコード回路」も重要な意味を持ちますが、これもここでは省略します。興味のある方は、筆者の「マイコン技術者スキルアップ事典」(CQ出版)など関連図書を参照して下さい。

マイコン回路の動作のもっとも重要なポイントとして、ここでは最後に「CPUが正しく動作するための条件」を確認しておきましょう。

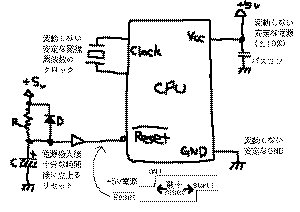
ソフトウェアも関係するとはいえ、CPUも一つのディジタルLSIなので、動作の条件はきわめてシンプルなものです。まずディジタル回路の最低条件として、

　・変動しない安定な電源

　・変動しない安定なGND

があります。

また、CPUの動作に不可欠なものとして、

　・安定な周波数のクロック信号

　・電源投入後、十分な時間後に立ち上がるリセット

という二つも最低限の必要条件です。CPUとはこのクロックに従って、プログラムで司令される内容を順番に実行しているだけのものですし、その正常なスタートは正しいリセット信号によって始まります。

電源回路と電池

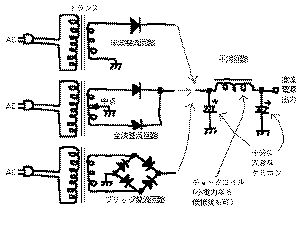
のようなトランスと整流回路とコンデンサによる平滑回路、ということになります。同じ商用AC電源入力が、トランスによって必要な電圧に変換され、それぞれの整流回路でどのような波形として出力されるかは、皆さんへの宿題とします。また、そのあとの平滑回路も、実は既に検討した積分回路、あるいはローパスフィルタの典型例ですので、これも動作について追いかけてみて下さい。

電源に関連した特殊な回路としては、「サイリスタ」という特殊な半導体を用いた「調光回路」があります。これは

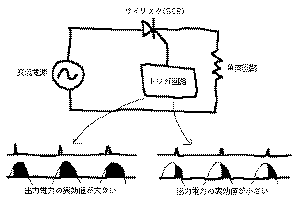
のように、交流電源の周期と同期して位相のずれたトリガ信号によって電力をスイッチングする素子で、連続的に負荷の電力を変化させることができるものです。電球の照明の明るさやヒーターの温度制御によく使われる回路なのですが、電力波形を見ると明らかなように、かなり急激に電力をスイッチングするので、周囲の電子回路に対しては強烈なノイズ源となります。基本的には、マイコンシステムのような繊細で過敏なシステムの近くには、このような回路が配置されないようにすることが重要です。

ディジタル機器の電源回路としてもっとも一般的なものは、

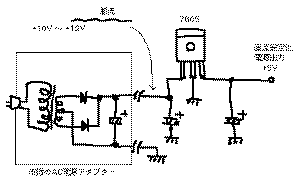
の「3端子レギュレータ」というICを用いた回路です。「整流－平滑回路」の出力というのは、極性としては単一であるものの、リップルという変動成分がかなり乗っているために、ディジタルICの動作条件である「安定して精度の高い直流電圧」という条件を満たしません。そこでこのような、内部に多数のトランジスタやツェナーダイオードによる「直流安定化回路」を組み込んだ3端子レギュレータICの利用は定石となっています。

電源回路にはこのレギュレータ電源と並んで、「スイッチング電源」と呼ばれる方式があります。これは、トランジスタやサイリスタのスイッチング回路によって、直流電源を高周波（数百KHzなどのオーダ）信号にしてしまい、電源につきものの大型トランスを省略して電力効率を上げたものです。この具体的な回路については深入りしませんが、省エネルギーの点では有効なものの、スイッチングによるノイズ源としてシステムにトラブルを招くことも多い、という点を指摘しておきましょう。

最後に、電源と並んで電子回路のエネルギー源となる「電池」について整理しておきます。電池には乾電池のように寿命まで使うだけの「1次電池」と、充電して何度も使える「2次電池」があります。1次電池としては、

　・マンガン乾電池（もっとも普通の電池）

　・アルカリ乾電池（出力電流容量が大きく寿命が長い）

　・ボタン型電池（リチウム、酸化銀などがある）

がよく使われています。006Pという9V電圧の乾電池も、中身は1.5Vのセルを直列にしているだけで同じものです。

また2次電池としては、これまでは「ニッカド電池」と呼ばれるニッケル・カドミウム電池が中心でしたが、最近の小型軽量の電子機器の実現を支えたものとして、

　・ニッケル水素電池

　・リチウムイオン電池

という新しいタイプが重要です。特にリイウムイオン電池は、完全放電しないで再充電を繰り返すと容量が低下してしまう「メモリ効果」の無い電池として、そして体積あたりのエネルギー密度の点で、小型パソコンや携帯電話を支えるキーテクノロジーとも言えるものです。