カオスに対する聴覚的なアプローチ (2)

長嶋洋一 (静岡文化芸術大学)

本日の内容

背景

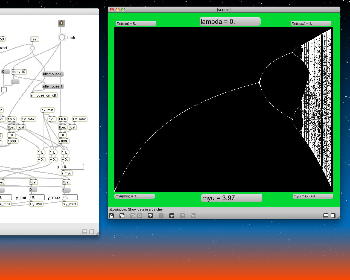
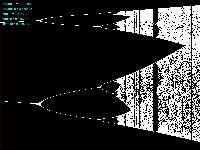
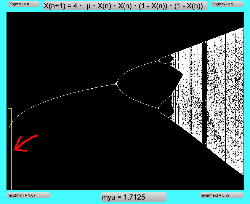
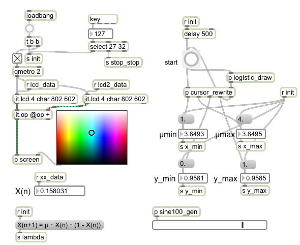
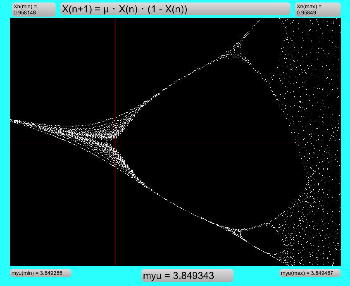
Logistic_06.maxpat

この Logistic_06.maxpat では、まず最初にμの範囲を「1.0から4.0」として、X(n)の値域は「0.0から1.0」として、ロジスティックマップを描画する。 そして描画完了すると、画面内のマウスカーソルの位置に横方向(μの軸)と縦方向(X(n)の軸)のラインが出るので、まずは拡大領域の「左上」の地点でマウスボタンを押し、拡大領域の「右下」の地点が刻々と矩形表示されるので、「ここでOK」という地点でマウスボタンを離す。 すると、その「左上」から「右下」の座標が新しいスクリーン領域として拡大描画される。

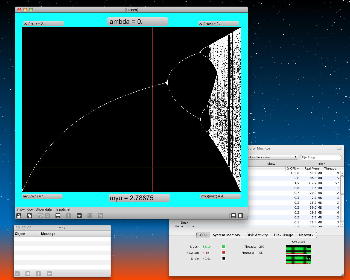
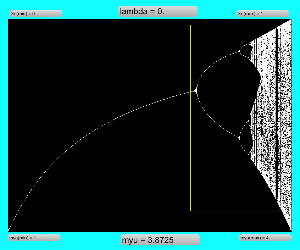
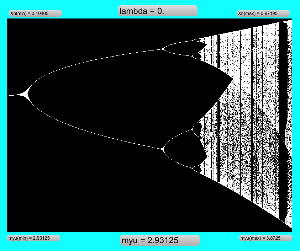
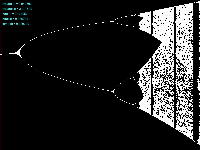
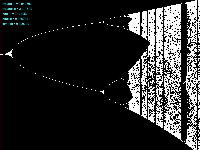
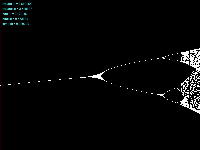
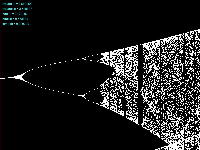
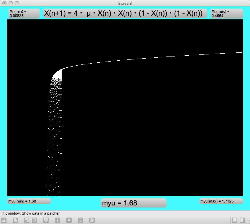
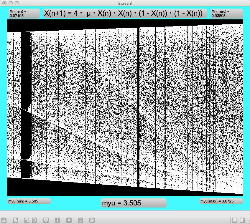
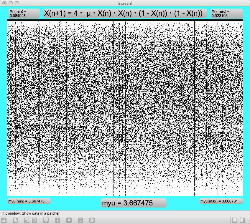
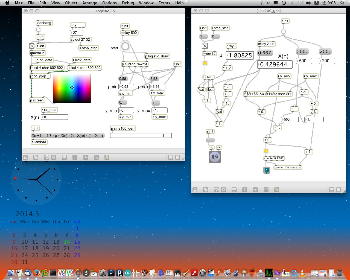
Logistic_08.maxpat

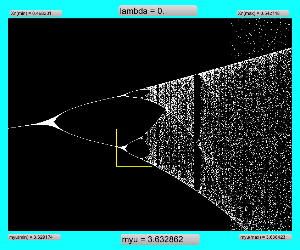
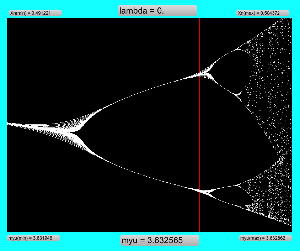
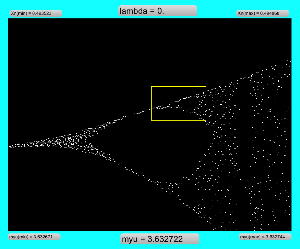
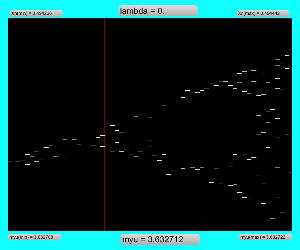
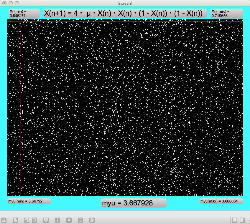
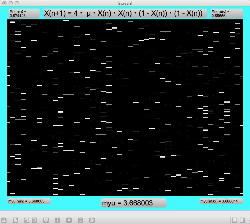
実験してみて判ったのは、「μ」と「X(n)」の変域の全域でも上述のアフィン変換のような拡大だったが、さらに領域拡大モードでオフセットがかかると、「λ」がゼロより大きい場合には、あまり全体に変化なく、単に画面外に出てしまい、どうやら、「λ」の導入はあまり効果が無さそう、と判明した。 以下は「λ」を刻々と刻んで連続スクリーンショットを撮る、という Logistic_08.maxpat。

以下に示したのは、「λ」を「0.02」、「0.01」、「0.0」と3パターンで刻んで、次第に拡大していったスクリーンショットの画面例である。 この例では敢えて中央付近で出現を避けたが、油断して拡大していくと画面が真っ黒になるのは、「λ」により値域が画面外(X(n)の最大値と最小値の範囲に入らない)場合である。

Logistic_10.maxpat

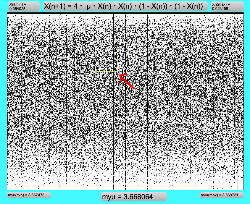
4次関数として、頂点X=0.5の場合にはX^4=0.25^2となることから、μをさらに4倍することにして、「X(n+1)=4・μ・X(n)・X(n)・(1-X(n))・(1-X(n))」とした Logistic_10.maxpat は以下のように、μの変域は「1≦μ≦4」よりも狭くなるものの、ロジスティックマップと類似したグラフを描画できた。

左端の立ち上がり部分を拡大表示してみると、これまでとちょっと違った振る舞いが見えた。

さらに、マップの右端のあたりをずんずんと拡大してみたのが、以下である。

Logistic_11.maxpat

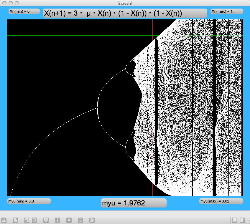
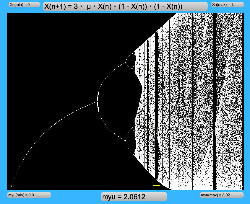
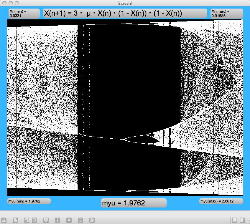
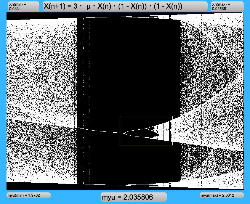
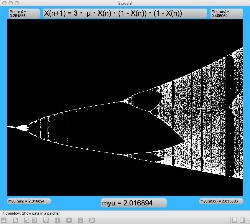
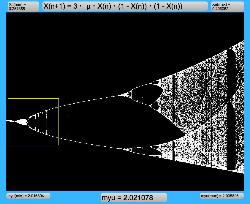
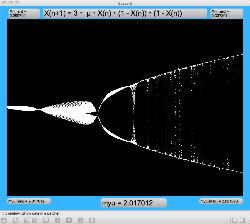
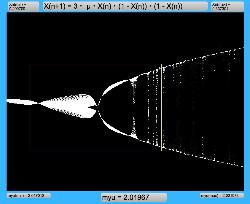
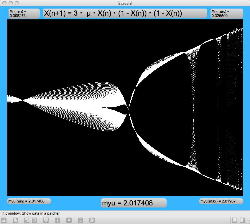
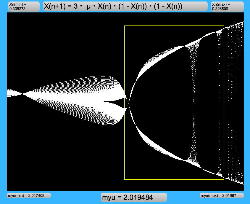
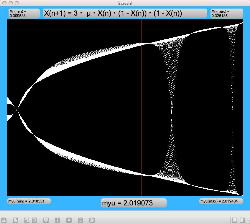
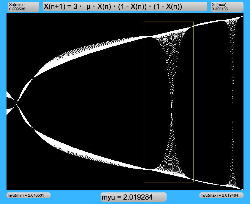
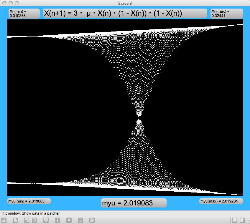
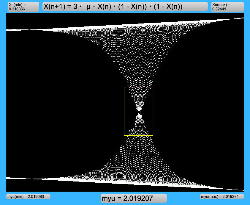
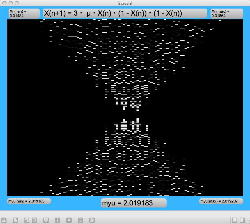
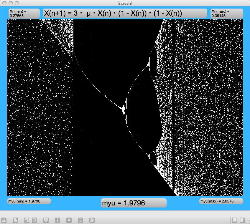
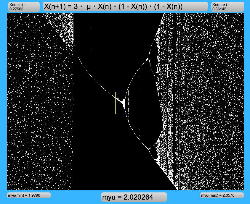
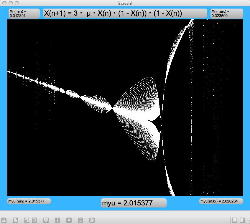
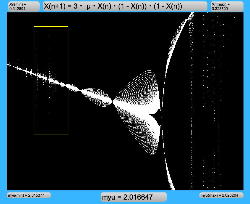
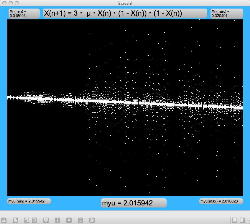
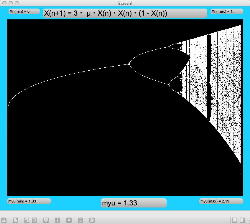
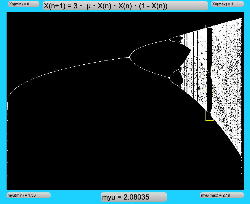
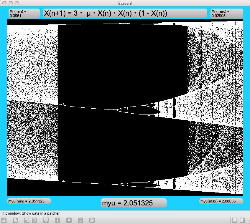
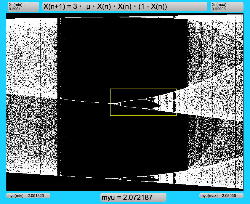
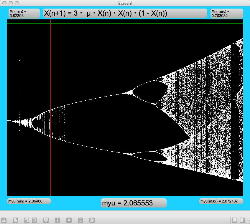
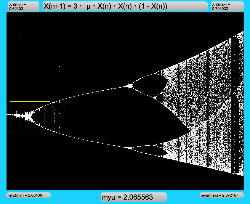
μを3倍して、「X(n+1)=3・μ・X(n)・(1-X(n))・(1-X(n))」とした Logistic_11.maxpat を試してみると、こちらもμの範囲はより限定する必要があるものの、以下のようにロジスティックマップと類似したグラフを描画できた。

4次と明らかに違う振る舞いがあったので、以下のようにぐりぐりと拡大してみた。

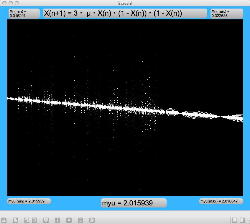
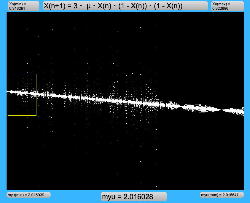
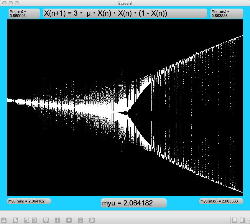
周期倍分岐のあたりに、何かトゲみたいなものが見えたので、さらにこの関数については、以下のように別の場所をスタートラインとして、ぐりぐりと拡大してみた。 こちらも計算精度の限界で荒くなるまで追いかけてみたが、やはり目新しいパターンがあった。

Logistic_12.maxpat

もう一つの3次関数のパターンとして、またまたμを3倍して、「X(n+1)=3・μ・X(n)・X(n)・(1-X(n))」とした Logistic_12.maxpat を試してみた。 こちらは上の例ほどの劇的なものではなく、これは二乗している項が「X(n)」であるか「(1-X(n))」であるか、の差であると思われる。

Logistic_14.maxpat

ズーミングに対応して、拡大した画面に表示されている値だけを、フルスケールでリマップして100個のサインオシレータで鳴らす、という Logistic_14.maxpat。 赤い縦線カーソルをぐりぐり左右に移動させてサウンドが変化する。

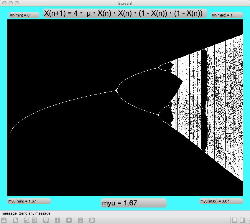
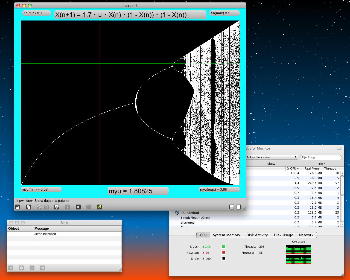
Logistic_15.maxpat

Logistic_14.maxpat が定番のロジスティックマップ「X(n+1)=μ・X(n)・(1-X(n))」だったので、「X(n+1)=3・μ・X(n)・(1-X(n))・(1-X(n))」という3次関数のバージョンも作った。 定数3は大きすぎるということで調整して、適当であるが「1.7」としたのが Logistic_15.maxpat である。

まとめと展望