BackgroundThis
compression algorithm is used for EEG data so that it can fit within
the 6kbps bluetooth bandwidth for the iPhone. This algorithm implements Golomb encoding which is ideal for signals of with a small rate of change. Consequently, to remain under the 6kbps bandwidth, a quantization
scheme is implemented on larger data changes to maintain a lower
bandwidth by rounding off the values. This makes the compression lossy
during quantization, but "heartbeat" packets(uncompressed EEG) will
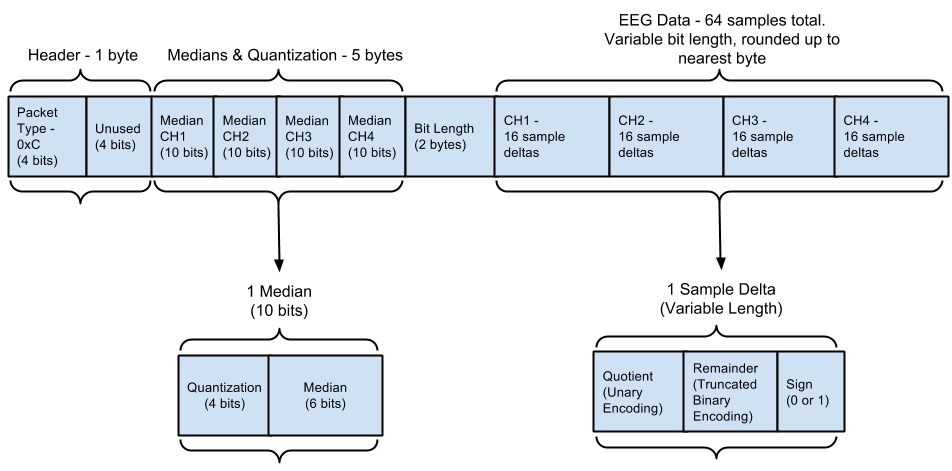
reset the values to the correct state. Overview of Packet SequenceAt the beginning of data transmission, an uncompressed EEG packet is sent. Following that, compressed EEG packets are sent with a heartbeat packet(uncompressed EEG) being sent every 8 compressed packets. This serves to eliminate accumulated error over time. If samples are dropped inside the Muse, an uncompressed packet is sent immediately. Every four packets a sync packet is sent(this is part of the legacy protocol and is technically not needed).When a compressed packet gets dropped within Muse, a heartbeat is sent immediately. This is because the decompression needs all samples to update it's reference values. All dropped samples are accounted for in the "dropped samples" value, so the dropped samples counter will start with a value of 16 and go up from there if more are dropped. Overview of AlgorithmThe compression algorithm works as follows:
The
first packet in the stream is sent uncompressed, giving the initial
values of the data. Each subsequent value is the difference from its
immediate predecessor. i.e. Dataset [20, 18, 11, 16, 16, 10, 4, 15] translates to [20, 2, 7, -5, 0, 6, 6, -11]. Encoding Sample-DeltasWe
use Golomb Encoding to send the sample-deltas, which is a lossless data
compression that has a small bit size when the value to be encoded is
small. The way the compression works is that a median for the
differences is found and then the difference data is broken into three
parts. The three parts of Golomb Encoding:
Computing the QuotientThe
quotient is a division of the current value by the absolute value of
the median. Using the above example, the median of the absolute values
is 6 (There are 7 values, median value index is [7 divided by 2 rounded
up] = 4, so the fourth value in [0,2,5,6,6,7,11] is 6). For the purposes
of the compression all differences will be in absolute(positive) value.
i.e. [2, 7, -5, 0, 6, 6, -11] will have quotients of [2/6, 7/6, 5/6, 0/6, 6/6, 6/6, 11/6] = [0, 1, 0, 0, 1, 1, 1] Encoding the QuotientUnary Code is a simple bit representation of the number with 1’s indicating it’s size.i.e. Unary Code of 5 is 111110, Unary Code of 1 is 10, and Unary code of 0 is 0. For quotients larger than 14(which should be rare), a simple dynamic encoding called Elias Gamma Encoding is used. Elias encoding starts with a unary encoded value of 15. This is followed by Elias encoding of the number, which is done through 0’s leading to the binary number indicating it’s bit length minus one(if the value is N bits long, prepend N-1 zeros to the value). i.e. "5" in Elias would be "00101", "85" would be "0000001010101". The whole sample of 85 would be 1111111111111110000001010101 instead of 85 1’s. Computing the RemainderThe remainder is the modulus of the value by the median. Using the sample above we have another set of data with varying remainders. i.e. [2, 7, -5, 0, 6, 6, -11] will have remainders of [2%6, 7%6, 5%6, 0%6, 6%6, 6%6, 11%6] = [2, 1, 5, 0, 0, 0, 5] Encoding the RemainderThe remainder is encoded using Truncated Binary Encoding.
Truncated Binary Encoding allows some remainders to be expressed with 1
less bit than the larger remainder values. Using an example of a median
of 6, following ceiling of log2(6) we know 3 bits are required to
represent values 0 through 5. Three bits have 8 states, therefore 8
available states minus 6 required states = 2 free unused states in 3
bits. This means we can represent the number 0 and 1 with 1 less bit
than 2, 3, 4 and 5. We do this by converting 0 and 1 to simply 00 and 01
respectively. However bits 2, 3, 4 and 5 are translated up by the free
state amount of 2. Therefore, 2 is 4, which is 100 and so on. Given this
example as follows. 0: 00 1: 01 2: 100 3: 101 4: 110 5: 111 Note that starting with 1 indicates that the value is not 0 or 1 ensuring all 3 bits included. To indicate how this might work for various other examples of 11, 23, and 9 follow.
Encoding the SignThe last bit is the value sign. If the difference is positive the bit is 0 and if it is negative the bit is 1.QuantizationThe quantization follows a fairly simple system of division. If the median from the data is too large is will divide it by a power of 2. If it remains too large it will divide by additional powers of 2.This particular case will do the following Median > 30, divide by 16 Median > 24, divide by 8 Median > 20, divide by 4 Median > 16 divide by 2 All of these divisions are completed in order, therefore if a division by 16 occurs then an additional division of 8, 4 or 2 may occur if the median continues to remain above any of the threshold in sequential order. The quantization is stored in the medians of each channel when sent to the parser. The first 4 bits are reserved for quantization. 10 bit Median: XXXX XXXXXX First 4 bits are used for quantization divisors, remaining 6 bits are used for median value. If the first bit is 1, value is divided by 16, if the second is 1, the value is again divided by 8, etc. Multiple bits can be 1 which increases quantization respectively. Will also send an uncompressed packet following the first good data packet to realign the absolute values for the individual channels. Implementation - Parsing Compressed EEG PacketsPseudo-code for Parsing Compressed DataNote: The “dropped samples” flag is not used in compressed EEG. Collect 4 Medians from bytes 1-5 (10 bits each, 40 bits total in 5 bytes) Extract Quantization values from Median data (the top 4 bits of the 10-bit medians). Medians are formatted least significant bits (LSB) first followed by most significant bits (MSB). Byte 1: XXXX XXXX (LSB Median 1) Byte 2: XXXX XXXX (Last 2 bits, MSB Median 1. First 6 bits, LSB Median 2) Byte 3: XXXX XXXX (Last 4 bits, MSB Median 2. First 4 bits, LSB Median 3) Byte 4: XXXX XXXX (Last 6 bits, MSB Median 3. First 2 bits, LSB Median 4) Byte 5: XXXX XXXX (MSB Median 4)
Loop through length of payload, bit by bit for each median If median is 0 all data for set is 0 (16 diffs in set) skip 16 * 3 bits, Quotient 0, remainder 0, sign 1 (0 is positive sign) move to next median/channel for 1 - 16 samples in current median (Parsing occurs bitwise in sequence) Parse Golomb-encoded value (See “Encoding Outline” below for more info) Parse Quotient Parse Remainder Parse Sign // After parsing, compute actual sample values: deltas = (quotient * median + remainder) * sign * quantization for each quotient in set Add delta to previous sample to get next sample The final sample should be stored as the starting values for the next compressed EEG packet. |
|
|