続・Propeller日記(3)

長嶋 洋一

Propeller日記(1)

Propeller日記(2)

Propeller日記(3)

Propeller日記(4)

Propeller日記(5)

続・Propeller日記(1)

続・Propeller日記(2)

続・Propeller日記(4)

続・Propeller日記(5)

続々・Propeller日記(1)

続々・Propeller日記(2)

続々・Propeller日記(3)

続々・Propeller日記(4)

2012年9月13日(木)

帰国後の9月13日、ただし午前2時である。 約2週間の渡欧ですっかり現地の時間になった身体は、寝不足でも日本時間の午前1-2時になれば、 現地では気持ち良く目覚めた「午前中」である。 21時前に帰宅して荷物を整理して22時半には就寝したが目覚めて眠れないので、 開き直って起き出してこれを書いている。(^_^;)

続・Propeller日記(2) の最後の部分を書いたのは成田までの機内だったが、成田では乗り継ぎが順調すぎてネットをアクセスできず、 セントレアに着いてもe-wingへの乗り継ぎが順調すぎて、メイルを確認しただけだった。 そこでここで起き出し、普段は自宅でやらないネット(PCは研究室なので普段は出来ない)に PHSからダイヤルアップで接続して、 とりあえずpart2をアップロードしたところである。 この部分は今日の朝、研究室に行ってからのアップロードとなる。

一つだけ思い出したことをメモする、というのが、これを深夜に書いている理由である。 OLED-PROPのグラフィックドライバにあった 

PUB plotCircle(_x0, _y0, _radius, _color) | sum, x, y
'' Plot a circle with center _x0,_y0 and radius _radius with the appropriate 8-bit color
''  _x0, _y0   - coordinate of the center of the circle
''  _radius    - radius, in pixels, of the circle
''  _color     - 8-bit color value (RRRGGGBB)
であるが、ProcessingやMaxに倣って、外接する矩形の頂点を指定して描画する、 というコマンドプロトコルを定義したが、せっかくなので、この「中心座標と半径」という指定についても、 別にコマンドプロトコルを定義しておくのもいいな、という点である。 考えてみれば楕円の描画をPropellerアセンブラでどうやるのか、けっこう難儀する可能性がある。 「円」であれば解析的に近似しやすいが、「楕円関数」というのはたしか、リーマン予想にまで繋がる、 数学史の巨大な山脈である。 いずれここに挑戦するとしても、まずは簡単に「円」を描画するコマンドを、 リファレンスとして用意するのは妥当である。

ここでちょっと悩んだのが、上のグラフィックドライバの「中心座標と半径と色」というパラメータである。 つまり、グラフィックドライバにそのまま与えるとすると、以下のようにパラメータは4つあり、 色指定はデータバイトの7ビットに収まらない。(^_^;)

  • 中心のX座標(0-95) 7ビット
  • 中心のY座標(0-63)　6ビット
  • 半径　7ビット?
  • 色指定(RRRGGGBB)　8ビット
ここでコマンドプロトコルを定義するには、以下の4つの方針がある。 いずれにしてもコマンド1発では無理である。
  • すでに定義した「今後の描画のカラー指定」の色情報を参照することを前提にして、「中心座標の指定(描画せず)」と「半径(1バイトはダミー)て描画」という2つのコマンドを用意する
  • すでに定義した「今後の描画のカラー指定」の色情報を参照することを前提にして、「半径(1バイトはダミー。描画せず)」「中心座標の指定で描画する」という2つのコマンドを用意する
  • ドット単位の座標とカラー指定のコマンドに倣って、「中心のX座標と半径の指定(描画せず)」と「[中心のY座標+カラーのMSB]と「カラーの下位7ビット]の指定で描画する」という2つのコマンドを用意する
  • ドット単位の座標とカラー指定のコマンドに倣って、「[中心のY座標+カラーのMSB]と「カラーの下位7ビット]の指定(描画せず)」と「中心のX座標と半径の指定で描画する」という2つのコマンドを用意する
これにはいずれも一長一短があり、けっこう悩ましい(^_^;)。 究極的には、アプリケーションとしてどういうグラフィクスを描画したいのか、というところにも関係する。 ランダム雨粒みたいな描画であればどれでも同じだが、 「半径違いの同心円」とか「同じサイズで色違いの円」とか「縦に並んだ円」とか「横に並んだ円」など、 使用する局面によって、連続して呼び出す場合には、全体としての効率がかなり違ってくるのである。

1番目と2番目は、今後、作っていく色々な描画コマンドと横並びで整然としているが、次々に色を変えたい場合には、 いちいちコマンドを3発、送らないといけなくなる。 3番目と4番目は、色まで含めてコマンド2発で完結しているが、呼び出し側では「画素単位の描画」の時のように、 けっこう面倒になってくる(^_^;)。

現在までに定義したコマンドで、残りの「reserved」を数えてみたら27個であった。 せっかくなので上記の4通りの全てを定義するとすれば、2つずつペアになった4種類、 つまり新たに計8つのコマンドを定義することになる。 まだ19個も残っているので一応はOKだが、けっこう混乱するかもしれない。 ペアとなっているコマンドは、(A)「指定して描画せず」と、(B)「指定して描画」とのセットであり、 連続して使用することで効率を上げたい場合には、共通の(A)に対して、(B)をいろいろ連発することになる。

ここで悩ましいのは、(B)が送られてきた時に、その前提である(A)は正しいペアとして指定されているか、 というのを、Propellerの方では感知できない点である。 最悪はかなり酷いことになると予想できる。 Propellerのプログラムはそういうエラーでは、コンパイラはエラーを出さないが、 実際には自分のワークメモリを上書きして暴走する自爆テロ状態となる(^_^;)。 実際、簡単な思考実験をすれば分かるように、上記の4種類のコマンドペアを適当に組み合わせたら、 座標の指定のところにカラー指定のビットが来たりするので、ぐちゃぐちゃになるのは確実である。 プログラマの自己責任、ということで規定するかどうか・・・悩ましい。(^_^;)

2012年9月16日(日)

上の9月13日(木)は、大学に行って未処理メイル1000本と格闘し、午後に出張報告や学生委員会などに追われて過ぎた。 翌9月14日(金)は、ようやくデジカメ写真6800枚の整理に取りかかるが、
  • 全ての画像をGraphicConverterで開く
  • ブレたりピンボケの画像を捨てるとともにHTMLソースからもカット(約3-4%)
  • 90度回転すべき画像はショートカットで回転
  • 全ての写真をショートカットで再保存
という作業のために、この日では完了しなかった。 また、先行して 上空から母校を発見 のページだけ作成した。 晩には個展の打合わせで卒業生の野口さんが来訪したので、お土産を渡した。

翌9月15日(日)は、ここ2週間まったく歌っていなかったので「この週末にカラオケ・・・」とのリュブリャナ空港での呟きに反応してくれた学生4人と、11-20時のマラソンカラオケを堪能した(^_^)。 朝、研究室で写真の処理が完了して、FTPでサーバにアップロードしたところ「所要時間・残り2時間40分」などと出たので(^_^;)、そのまま放置して大学からBIG ECHOに向かった。 今回は、遂に「25.2kcal」という自己最高記録が出たのが収穫であった。

そしてようやく、9月16日(日)である。 午前には色々と修正しつつ 欧州ツアー2012 のページが完成した。末尾には、日々刻々と飲みまくったビールとワインを並べたが、こうして見ると、うーーーむ、よく飲んだ(^_^;)。

そして、予想されていたように、Propellerについては、まだまだ着手できないのであった。 日々、先にこなすべき事項が山積している。なんとか復活したいが、しばらく先になりそうである。

2012年9月17日(月/祝)

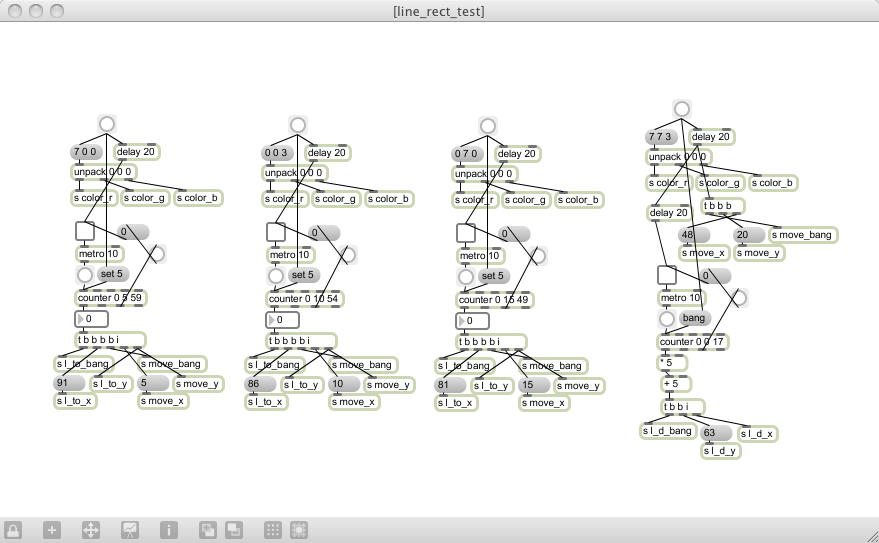
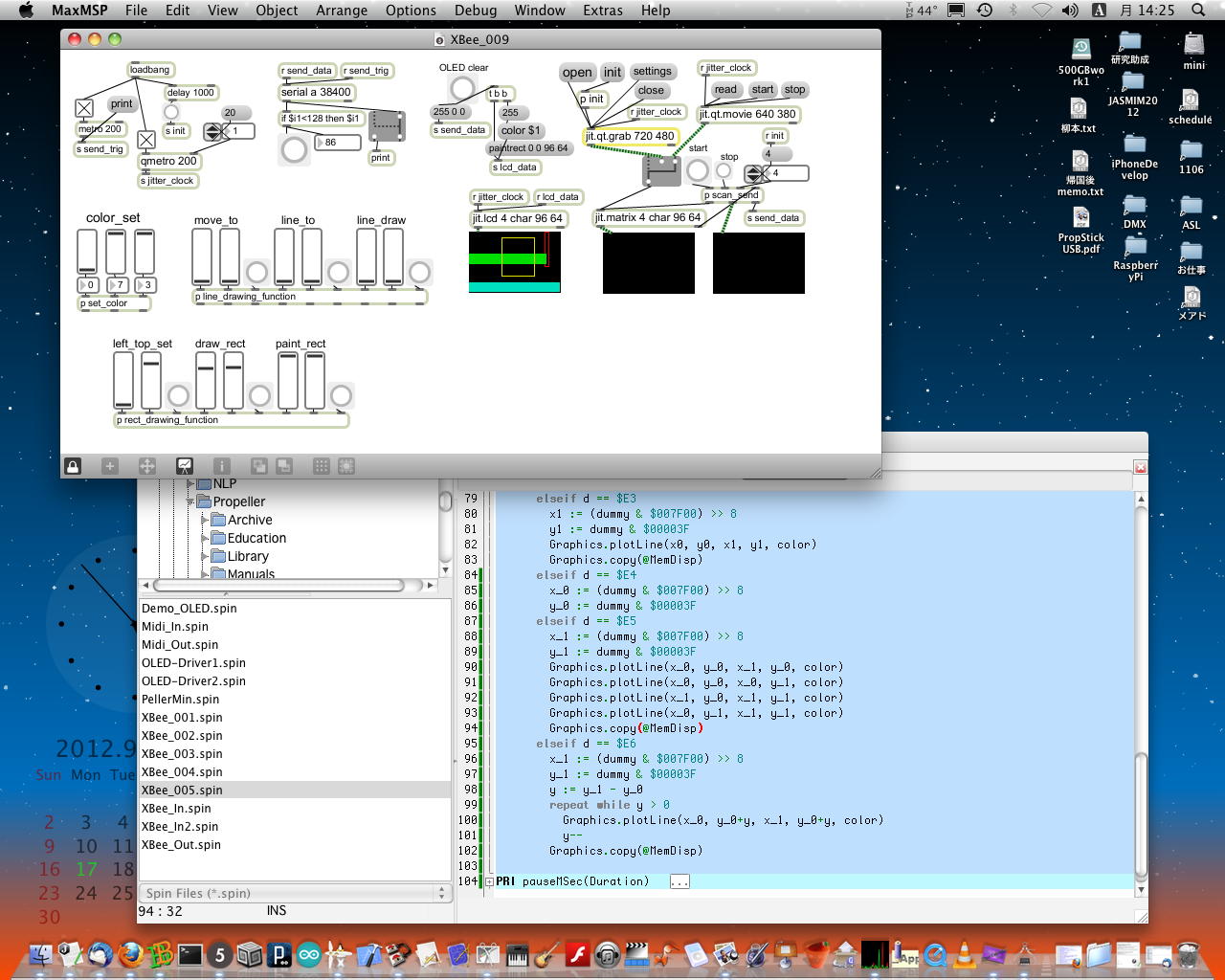
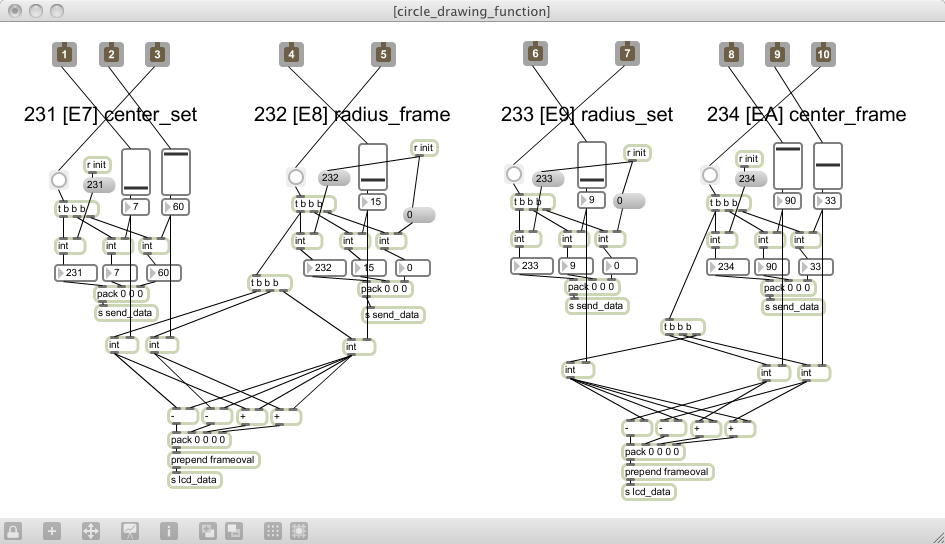
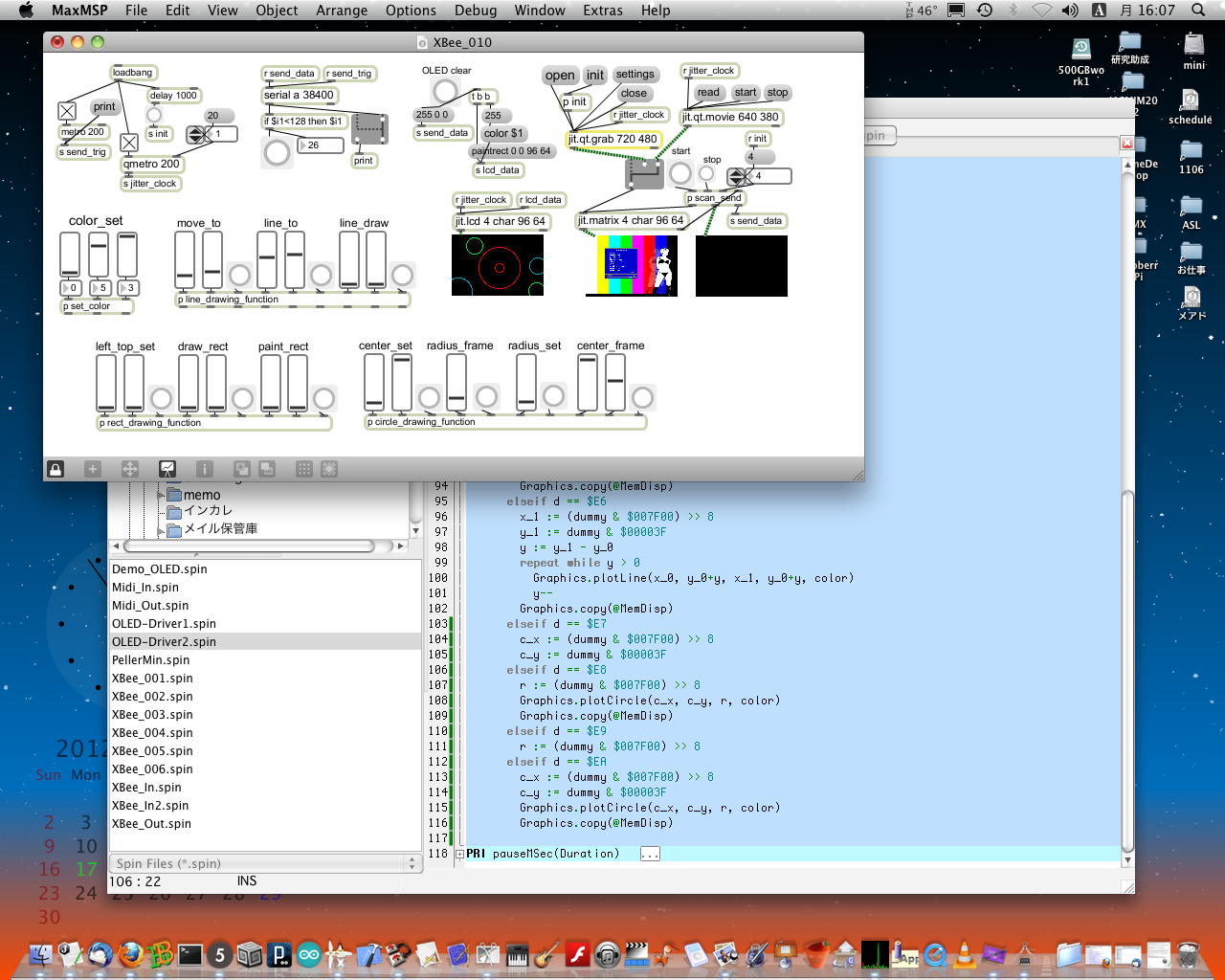
昨日「しばらく先になりそう」と書いたその翌日は、なんと祝日だった(^_^;)。 SUACはお役所なので休日祝日は完全停止、宅急便も郵便も届かず事務作業も出来ない。 そうなれば、研究室であれこれ三昧という事になる。これを「Propeller日和」という(^_^)。 仕掛っていたコマンドプロトコルに関して、寝かせていれば熟成するもので、 ちょっと頭の中で整理できてきたので、途中まで進めてみることにした。 まずは以下のように、2週間ぶりの研究室のお仕事Macにセッティングである。 やはり、2画面あると、まさに「お店を広げる」カンジで、やりやすい(^_^)。 Mac miniなので、カメラはFireWire経由でiSightを繋いでみた。

引き続き、窮屈なMacBookAirでやりくりして詰め込んできたパッチを開いて、以下のように、 ライン描画コマンドをMaxの側で繰り返して矩形を描画した実験の部分を、サブパッチとして収めた。 これでスッキリしたので、まだまだ作っていける(^_^)。

「仕掛っていたコマンドプロトコルに関して、寝かせていれば熟成するもので、ちょっと頭の中で整理できてきた」と書いたが、 ここでまとめてみよう。 「続・Propeller日記(2)」 の9月12日の後半で検討したのは、「矩形の描画」と「楕円の描画」についてであり、それぞれ「輪郭」と「塗りつぶし」、 計4種類のコマンドであった。 そしてこの4種類に共通して、「左上の座標の指定(描画しない)」というものを規定した。 この全5種類のコマンドの定義に続いて、この「続・Propeller日記(3)」の冒頭、9月13日に検討したのが、 OLED-PROPのグラフィックドライパが標準で持っている、「円の輪郭の描画」を使わない手は無い、ということで、 「中心座標」「半径」「色」を指定するための方法が4通り(コマンドは8種類)ほどある(いずれも一長一短ある)、という事だった。

そして、熟成(夜中に目覚めてうつらうつらと検討)した整理を、以下にまとめる。 9月12日の後半で定義したコマンド番号は変更になるが、まだ「絵に描いた餅」の状態だったので、 これはいくらでも変更できる。既にPropellerに書き込んだライン描画系については変更しない。 新たに気付いた(思い出した)のは、矩形を描画する方法について。

  • 既に実験したように、Maxの側で矩形の座標を解釈して「line」系としてXBeeで送る
  • XBeeでコマンドを受けたPropellerの方のspinプログラムとして矩形の座標を解釈してドライバを呼ぶ
  • Maxからはシンプルに定義したコマンドをXBeeで送り、Propellerのspinプログラムはシンプルにドライバを呼び出し、新たなグラフィックドライパを追加してアセンブラで矩形の座標を解釈して描画する
と書いたところで、 「この3番目の方法は、たぶんもっとも大変だが、たぶんもっとも高速である」と書いたのは、まぁ正しい。 ただし、よく見てみたら、OLED-PROPのグラフィックドライパも直線とか円とかは、 アセンブラでなくspinで記述していた(^_^;)。 これも含めて、問題は「2番目のspinうにゃうにゃも、あまり美しくない」という部分の間違いであった。 Propellerのプログラムは、spin言語仕様はPropeller専用にチューニングされているので、 C言語などのようにコンパイラ言語をアランブラに変換する際の無駄が無いのである。 つまり、アセンブラで書いても、spinで書いても、あまりスピードは変わらないのであった。 となれば、矩形の描画は、上の3通りの2番目がもっとも効率が良い。 矩形の輪郭は座標から4頂点を得て4本のラインを呼び出せばいいし、 塗りつぶしはライン描画をspinで記述してループで回せばいい。 ただし楕円についてはまったく別なので、これは切り離して考えるべきである。

一方、9月13日に悩んだ「円」であるが、これはせっかくOLED-PROPの標準グラフィックドライパが「中心座標」「半径」「色」でサポートしているので、こちらもspinで記述して活用すべきなのだった。 4通り、それぞれ一長一短があるとすれば、コマンドを8種類(塗りつぶしがあったので倍の16種類だった)、全て定義してしまえばよい。 輪郭はドライパ一発、そして塗りつぶしも半径を1までspinループで回して減らせばいい。 結局、楕円だけが難しいので、これを将来に先送りして(^_^;)、そこまでを完備してしまおう、という事である。 これは、たまたま「Propeller日和」となった休日に相応しい、楽しいお仕事である。(^_^)

・・・ということで、またまた教条主義的ではあるが、これまでに定義したコマンドプロトコルに加えて、 以下のように定義を改訂増補してみた。 きっちりとしたコマンドの定義なくして、Maxでコマンドを送るためのプログラミングも、ましてPropeller側で受けるプログラミングも出来ないからである。 棚上げの「楕円」を最後に持っていって、コマンド番号の若い方から詰めていくために、 以前の定義から移動している部分があるので、今後はこちらを参照していこう。 8種類でなく16種類、と書いたが、定義部分は共用できるので12種類に・・・という可能性も検討したが、 たぶんプログラミングの現場で混乱しそうなので、敢えて冗長に16種類とした。 ちょっと悩んだ「プログラマの自己責任」(ペアとなっているコマンド)の部分であるが、まさにプログラマの自己責任ということで行く。(^_^;)

  • メッセージは全て3バイトを単位とする
  • 先頭データ(ステータスバイト)のMSBは1で、続く2バイトのデータバイトは7ビットデータ(0-127)
  • ステータスバイト「%10000000」-「%110111111」 - 画素単位のカラー描画
    • カラーは「8-bit color value (RRRGGGBB)」と定義
    • ステータスバイトの下位7ビットがOLEDのX座標(0-95)
    • 2バイト目のデータバイト(7ピット)の下位6ビット(bit 5-0)がOLEDのY座標(0-63)
    • 2バイト目のデータバイト(7ピット)のbit 6がカラーのMSB
    • 3バイト目のデータバイト(7ビット)にこのカラーのMSBを加えた8ビットが、その画素のカラー(RRRGGGBB)
  • ステータスバイト「%11100000」 - color_set (後の描画コマンドでのカラー指定)
    • このコマンドでは描画しない。後の各種描画コマンドのための共通のカラー指定
    • 2バイト目のデータバイト(7ピット)のLSB、つまりbit 0がカラーのMSB
    • 3バイト目のデータバイト(7ビット)にこのカラーのMSBを加えた8ビットをカラー(RRRGGGBB)とする
    • このコマンドが指定される前の初期値はゼロ(真っ黒)
  • ステータスバイト「%11100001」 - move_to (ラインを引く起点の座標の指定)
    • このコマンドでは描画しない。「line_to」と「line_draw」コマンドのための起点座標指定
    • 2バイト目のデータバイト(7ピット)がラインを引く起点のX座標
    • 3バイト目のデータバイト(7ビット)がラインを引く起点のY座標
    • このコマンドが指定される前の初期値は(0,0)
  • ステータスバイト「%11100010」 - line_to (ラインを引き終点を新しい起点とする)
    • 2バイト目のデータバイト(7ピット)がラインを引く終点のX座標
    • 3バイト目のデータバイト(7ビット)がラインを引く終点のY座標
    • ラインを引くカラーは最後に「color_set」で指定されたカラー(RRRGGGBB)
    • 終点座標を指定してラインを指定カラーで描画し、終点座標を起点座標に代入する
  • ステータスバイト「%11100011」 - line_draw (ラインを引き起点はそのまま)
    • 2バイト目のデータバイト(7ピット)がラインを引く終点のX座標
    • 3バイト目のデータバイト(7ビット)がラインを引く終点のY座標
    • ラインを引くカラーは最後に「color_set」で指定されたカラー(RRRGGGBB)
    • 終点座標を指定してラインを指定カラーで描画し、起点座標はそのまま変化させない
  • ステータスバイト「%11100100」 - rect_start (矩形の左上の座標の指定)
    • 矩形または楕円を描画するための左上の座標を共通に指定する
    • このコマンドでは描画しない。「frame_rect」と「paint_rect」と「frame_oval」と「paint_oval」コマンド用の左上の座標指定
    • 2バイト目のデータバイト(7ピット)が矩形指定の左上のX座標
    • 3バイト目のデータバイト(7ビット)が矩形指定の左上のY座標
    • このコマンドが指定される前の初期値は(0,0)
  • ステータスバイト「%11100101」 - frame_rect (矩形の輪郭の右下の座標と描画)
    • 2バイト目のデータバイト(7ピット)がラインで矩形を描画する右下のX座標
    • 3バイト目のデータバイト(7ビット)がラインで矩形を描画する右下のY座標
    • ラインを引くカラーは最後に「color_set」で指定されたカラー(RRRGGGBB)
    • 「rect_start」で指定された左上の座標に対してラインで矩形を描画する
    • 左上の座標より必ず右下にあること(チェックしない)
  • ステータスバイト「%11100110」 - paint_rect (塗りつぶしの矩形の右下の座標と描画)
    • 2バイト目のデータバイト(7ピット)が塗りつぶしの矩形を描画する右下のX座標
    • 3バイト目のデータバイト(7ビット)が塗りつぶしの矩形を描画する右下のY座標
    • 塗りつぶしのカラーは最後に「color_set」で指定されたカラー(RRRGGGBB)
    • 「rect_start」で指定された左上の座標に対して塗りつぶしで矩形を描画する
    • 左上の座標より必ず右下にあること(チェックしない)
  • ステータスバイト「%11100111」 - frame_circle1a (円の輪郭のための中心座標の指定)
    • このコマンドでは描画しない。「frame_circle1b」コマンドのための起点座標指定(必ず先に指定すること)
    • 2バイト目のデータバイト(7ピット)が円の中心のX座標
    • 3バイト目のデータバイト(7ビット)が円の中心のY座標
  • ステータスバイト「%11101000」 - frame_circle1b (円の輪郭のための半径の指定と描画)
    • 先に必ず「frame_circle1a」コマンドで円の中心座標が指定されていること
    • 2バイト目のデータバイト(7ピット)が描画する円の半径
    • 3バイト目は無視
    • 半径は必ず1以上であること(チェックしない)
    • 円の輪郭のカラーは最後に「color_set」で指定されたカラー(RRRGGGBB)
    • 「frame_circle1a」で指定された中心座標に対して、指定された半径の円の輪郭を描画する
  • ステータスバイト「%11101001」 - frame_circle2a (円の輪郭のための半径の指定)
    • このコマンドでは描画しない。「frame_circle2b」コマンドのための半径指定(必ず先に指定すること)
    • 2バイト目のデータバイト(7ピット)が描画する円の半径
    • 3バイト目は無視
    • 半径は必ず1以上であること(チェックしない)
  • ステータスバイト「%11101010」 - frame_circle2b (円の輪郭のための中心座標の指定と描画)
    • 先に必ず「frame_circle2a」コマンドで円の半径が指定されていること
    • 2バイト目のデータバイト(7ピット)が円の中心のX座標
    • 3バイト目のデータバイト(7ビット)が円の中心のY座標
    • 円の輪郭のカラーは最後に「color_set」で指定されたカラー(RRRGGGBB)
    • 「frame_circle2a」で指定された半径に対して、指定された中心座標の円の輪郭を描画する
  • ステータスバイト「%11101011」 - frame_circle3a (円の輪郭のための中心のX座標と半径の指定)
    • このコマンドでは描画しない。「frame_circle3b」コマンドのための指定(必ず先に指定すること)
    • 2バイト目のデータバイト(7ピット)が円の中心のX座標
    • 3バイト目のデータバイト(7ビット)が描画する円の半径
    • 半径は必ず1以上であること(チェックしない)
  • ステータスバイト「%11101100」 - frame_circle3b (円の輪郭のための中心のY座標とカラーの指定と描画)
    • 先に必ず「frame_circle3a」コマンドで中心のX座標と円の半径が指定されていること
    • 2バイト目のデータバイト(7ピット)の下位6ビット(bit 5-0)が円の中心のY座標(0-63)
    • 2バイト目のデータバイト(7ピット)のbit 6がカラーのMSB
    • 3バイト目のデータバイト(7ビット)にこのカラーのMSBを加えた8ビットが、円の輪郭を描画するカラー(RRRGGGBB)
    • 「frame_circle3a」で指定されたX座標と半径に対して、指定されたY座標とカラーの円の輪郭を描画する
  • ステータスバイト「%11101101」 - frame_circle4a (円の輪郭のための中心のY座標とカラーの指定)
    • このコマンドでは描画しない。「frame_circle4b」コマンドのための指定(必ず先に指定すること)
    • 2バイト目のデータバイト(7ピット)の下位6ビット(bit 5-0)が円の中心のY座標(0-63)
    • 2バイト目のデータバイト(7ピット)のbit 6がカラーのMSB
    • 3バイト目のデータバイト(7ビット)にこのカラーのMSBを加えた8ビットが、円の輪郭を描画するカラー(RRRGGGBB)
  • ステータスバイト「%11101110」 - frame_circle4b (円の輪郭のための中心のX座標と半径の指定と描画)
    • 先に必ず「frame_circle4a」コマンドで中心のY座標とカラーが指定されていること
    • 2バイト目のデータバイト(7ピット)が円の中心のX座標
    • 3バイト目のデータバイト(7ビット)が描画する円の半径
    • 半径は必ず1以上であること(チェックしない)
    • 「frame_circle4a」で指定されたY座標とカラーに対して、指定されたX座標と半径の円の輪郭を描画する
  • ステータスバイト「%11101111」 - paint_circle1a (塗りつぶし円のための中心座標の指定)
    • このコマンドでは描画しない。「paint_circle1b」コマンドのための起点座標指定(必ず先に指定すること)
    • 2バイト目のデータバイト(7ピット)が塗りつぶし円の中心のX座標
    • 3バイト目のデータバイト(7ビット)が塗りつぶし円の中心のY座標
  • ステータスバイト「%11110000」 - paint_circle1b (塗りつぶし円のための半径の指定と描画)
    • 先に必ず「paint_circle1a」コマンドで円の中心座標が指定されていること
    • 2バイト目のデータバイト(7ピット)が描画する塗りつぶし円の半径
    • 3バイト目は無視
    • 半径は必ず1以上であること(チェックしない)
    • 塗りつぶし円のカラーは最後に「color_set」で指定されたカラー(RRRGGGBB)
    • 「paint_circle1a」で指定された中心座標に対して、指定された半径の塗りつぶし円を描画する
  • ステータスバイト「%11110001」 - paint_circle2a (塗りつぶし円のための半径の指定)
    • このコマンドでは描画しない。「paint_circle2b」コマンドのための半径指定(必ず先に指定すること)
    • 2バイト目のデータバイト(7ピット)が描画する塗りつぶし円の半径
    • 3バイト目は無視
    • 半径は必ず1以上であること(チェックしない)
  • ステータスバイト「%11110010」 - paint_circle2b (塗りつぶし円のための中心座標の指定と描画)
    • 先に必ず「paint_circle2a」コマンドで塗りつぶし円の半径が指定されていること
    • 2バイト目のデータバイト(7ピット)が塗りつぶし円の中心のX座標
    • 3バイト目のデータバイト(7ビット)が塗りつぶし円の中心のY座標
    • 塗りつぶし円のカラーは最後に「color_set」で指定されたカラー(RRRGGGBB)
    • 「frame_paint2a」で指定された半径に対して、指定された中心座標の塗りつぶし円を描画する
  • ステータスバイト「%11110011」 - paint_circle3a (塗りつぶし円のための中心のX座標と半径の指定)
    • このコマンドでは描画しない。「paint_circle3b」コマンドのための指定(必ず先に指定すること)
    • 2バイト目のデータバイト(7ピット)が塗りつぶし円の中心のX座標
    • 3バイト目のデータバイト(7ビット)が描画する塗りつぶし円の半径
    • 半径は必ず1以上であること(チェックしない)
  • ステータスバイト「%11110100」 - paint_circle3b (塗りつぶし円のための中心のY座標とカラーの指定と描画)
    • 先に必ず「paint_circle3a」コマンドで中心のX座標と塗りつぶし円の半径が指定されていること
    • 2バイト目のデータバイト(7ピット)の下位6ビット(bit 5-0)が塗りつぶし円の中心のY座標(0-63)
    • 2バイト目のデータバイト(7ピット)のbit 6がカラーのMSB
    • 3バイト目のデータバイト(7ビット)にこのカラーのMSBを加えた8ビットが、円の輪郭を描画するカラー(RRRGGGBB)
    • 「frame_paint3a」で指定されたX座標と半径に対して、指定されたY座標とカラーの塗りつぶし円を描画する
  • ステータスバイト「%11110101」 - paint_circle4a (塗りつぶし円のための中心のY座標とカラーの指定)
    • このコマンドでは描画しない。「paint_circle4b」コマンドのための指定(必ず先に指定すること)
    • 2バイト目のデータバイト(7ピット)の下位6ビット(bit 5-0)が塗りつぶし円の中心のY座標(0-63)
    • 2バイト目のデータバイト(7ピット)のbit 6がカラーのMSB
    • 3バイト目のデータバイト(7ビット)にこのカラーのMSBを加えた8ビットが、塗りつぶし円の輪郭を描画するカラー(RRRGGGBB)
  • ステータスバイト「%11110110」 - paint_circle4b (塗りつぶし円のための中心のX座標と半径の指定と描画)
    • 先に必ず「paint_circle4a」コマンドで中心のY座標とカラーが指定されていること
    • 2バイト目のデータバイト(7ピット)が塗りつぶし円の中心のX座標
    • 3バイト目のデータバイト(7ビット)が描画する塗りつぶし円の半径
    • 半径は必ず1以上であること(チェックしない)
    • 「frame_paint4a」で指定されたY座標とカラーに対して、指定されたX座標と半径の塗りつぶし円を描画する
  • ステータスバイト「%11110111」
  • ステータスバイト「%11111000」
  • ステータスバイト「%11111001」
  • ステータスバイト「%11111010」
  • ステータスバイト「%11111011」
  • ステータスバイト「%11111100」
  • ステータスバイト「%11111101」 - frame_oval (楕円の輪郭に外接する矩形の右下の座標と描画)
    • 2バイト目のデータバイト(7ピット)がラインで楕円を描画する外接矩形の右下のX座標
    • 3バイト目のデータバイト(7ビット)がラインで矩形を描画する外接矩形の右下のY座標
    • ラインを引くカラーは最後に「color_set」で指定されたカラー(RRRGGGBB)
    • 「rect_start」で指定された左上とこの右下の座標の矩形に内接する楕円の輪郭を描画する
    • 左上の座標より必ず右下にあること(チェックしない)　※spinでチェックする???
  • ステータスバイト「%11111110」 - paint_oval (塗りつぶしの楕円に外接する矩形の右下の座標と描画)
    • 2バイト目のデータバイト(7ピット)が塗りつぶしで楕円を描画する外接矩形の右下のX座標
    • 3バイト目のデータバイト(7ビット)が塗りつぶしで矩形を描画する外接矩形の右下のY座標
    • 塗りつぶしのカラーは最後に「color_set」で指定されたカラー(RRRGGGBB)
    • 「rect_start」で指定された左上とこの右下の座標の矩形に内接する楕円を塗りつぶしで描画する
    • 左上の座標より必ず右下にあること(チェックしない)　※spinでチェックする???
  • ステータスバイト「%11111111」 - OLED全画面をクリア(→真っ黒) - 2/3バイト目は無視

よく「数学が苦手なのでプログラミングは苦手です」という人がいるが、それは間違いである。 上記のように、論理的に矛盾なく仕様を完備するのは「数学」でなく「国語」であり、 これを整理しているうちに、頭の中ではほぼプログラミング(アルゴリズム)は完成している。 残りreservedは6種類になったが、だいぶ整理されてきた。 ここまでの仕様を整理する時間と、実際にMax側とPropeller側でプログラムを実装する時間とは、それほどあまり変わらない筈である。

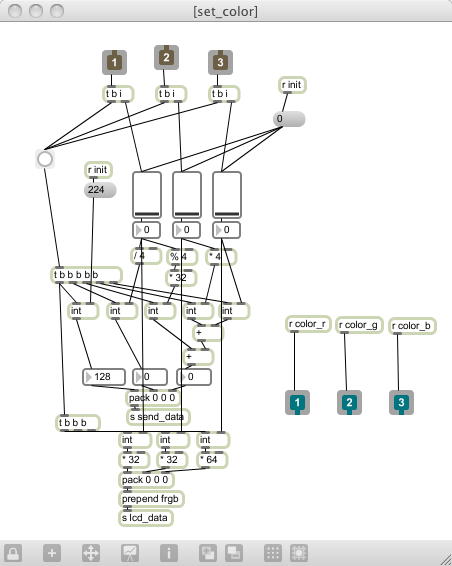
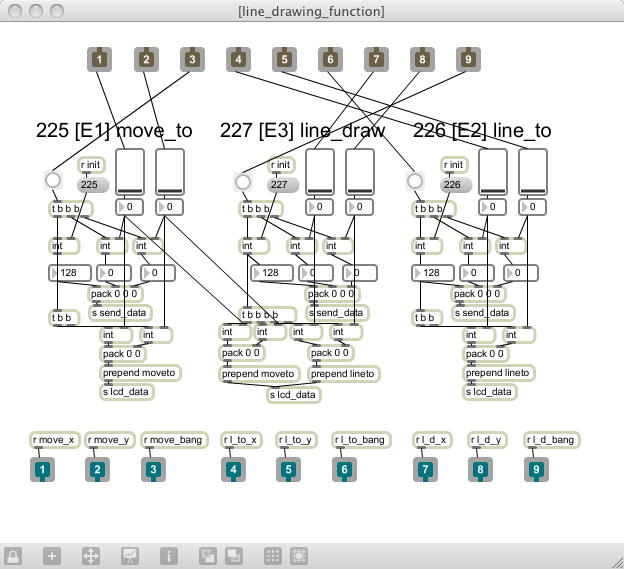
「円」に関する16種類のコマンドに加えて、spinで矩形を描画する3種類もあったので、計19個もある。 単にXBeeからこの「絵に描いた餅」のコマンド(パラメータ)を送るだけでなく、Max側のjitterウインドウにも描画する、 という機能も、デバッグのために完備しておきたい。 ここは既に出来ている以下の2つの「set_color」と「line_drawing_function」というサブパッチを参考に、じっくりと作っていくことにした。

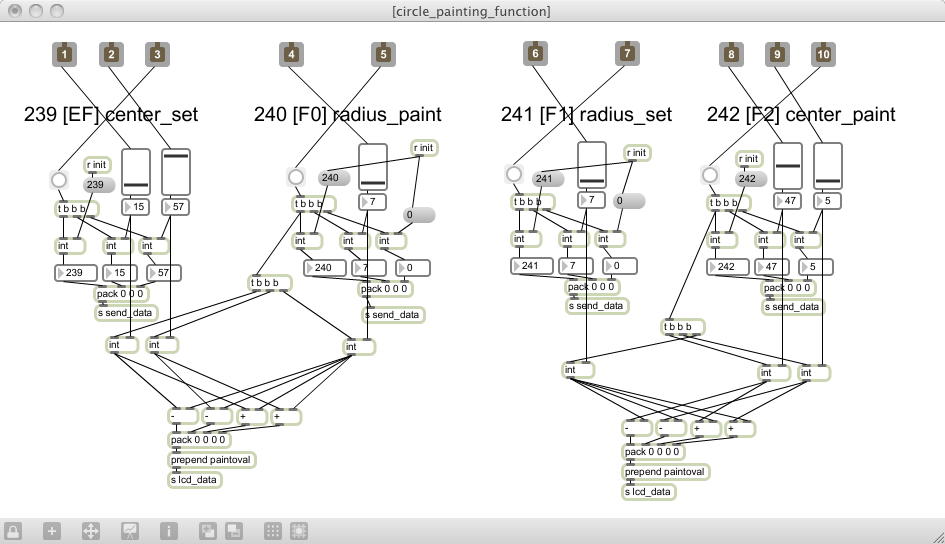
まず第一段階として、以下のようにMaxの送り側で、「rect_drawing_function」というサブパッチを作り、 XBee経由で矩形の「座標指定」「輪郭描画」「塗りつぶし描画」の3つのコマンドを送る(画面内に描画)、 という「つもり」が出来上がった。

これに続いてbstを開いて、Propellerの側でspinプログラム部分を拡充して、XBee経由で同じ矩形の描画を実現すればいい事になる。 久しぶりにspinのループが必要になり、「あ、for文が無い(^_^;)」とマニュアルを引っ張り出して、 「あ、repeatというのがあった(^_^;)」などと思い出しタイムを経て、無事に、以下のように「矩形の描画」と「矩形の塗りつぶし」が出来た。

こうなれば、あとは一気に「円」関係である。 Maxのパッチを「XBee_009.maxpat」から「XBee_010.maxpat」、 Propellerのプログラムを「XBee_005.spin」から「XBee_006.spin」に上げて、 まずは、共通のカラーで、円の輪郭を描画するために中心座標と半径を指定する2種類4コマンドを作ってみた。 Maxのjit.lcdでは、外接する矩形で楕円を表現するので、中心座標に対して半径を加算/減算して頂点の座標を計算している。 以下のように、OLEDでは画面をハミ出た場合には、折り返して描画してくるが、 これもプログラマの責任である(^_^;)。

引き続き、「塗りつぶし円」である。 Maxのパッチを「XBee_010.maxpat」から「XBee_011.maxpat」、 Propellerのプログラムを「XBee_006.spin」から「XBee_007.spin」に上げて、 共通のカラーで、塗りつぶし円を描画するために中心座標と半径を指定する2種類4コマンドを作ってみた。 Maxのjit.lcdの方では、「frameoval」を「paintoval」に変更するだけであるが、 Propellerの方では、半径が1になるまでデクリメントする、というループを回すことになる。 以下のように、こちらも簡単に実現できた。(^_^)

・・・とここまで来て、残った「中心座標」「半径」「カラー」の指定の4種類、8コマンドの部分で、ちょっとストップした。 Propellerの方のプログラムは以下のように、コマンドごとに変数バッファを持っているので、 そのまま延長して拡張していけばいいのだが、Maxの方(jit.lcd)のモニタ画面の描画に関しては、 これまで作ったサブパッチでは、全て共通にカラー指定を行っていた事に気付いた。 これはMaxでは基本のイベント主義、つまり「最後に指定された情報が有効」というものだが、 ここまでに定義したコマンドと、新たに円ごとにカラー指定をした場合、Propellerの方ではちゃんと受けられるのに対して、 Maxの方(jit.lcd)のモニタ画面では、カラー情報が上書きされるので、そのままではいかない(^_^;)。 ちょっとMax側で、カラーを記憶しておくメカニズムを、いくつものサブパッチに対して横断的に新設する必要がある。 これは、ちょうど「また後日」というタイミングだろう、と判断して、以下に現在の「XBee_007.spin」を置いて、 今日はここまでにしよう。 あれこれ、何故か高校や中学の同窓会関係のメイルが行き来している中で、なかなかに進んだということで。(^_^;) 
CON
  _clkmode = xtal1 + pll8x      'Use the PLL to multiple the external clock by 8
  _xinfreq = 8_000_000          'An external clock of 8MHz. is used (64MHz. operation)
  _OUTPUT       = 1             'Sets pin to output in DIRA register
  _INPUT        = 0             'Sets pin to input in DIRA register  
  _HIGH         = 1             'High=ON=1=3.3v DC
  _ON           = 1
  _LOW          = 0             'Low=OFF=0=0v DC
  _OFF          = 0
  _ENABLE       = 1             'Enable (turn on) function/mode
  _DISABLE      = 0             'Disable (turn off) function/mode
  _xpixels      = 96                                    'Screen width
  _ypixels      = 64                                    'Screen height          
  _pixelperlong = 4                                     'Each tile requires 4 longs
  _xtiles       = _xpixels/_pixelperlong                'Each tile is 4 pixels x 4 pixels
  _ytiles       = _ypixels/_pixelperlong                                        
  _screensize   = (_xtiles * _ytiles * _pixelperlong)   'Size needed for arrays
  _red          = %11100000
  _green        = %00011100
  _blue         = %00000011
  _yellow       = %11111100
  _purple       = %11100011
  _turq         = %00011111
  _white        = %11111111
  _black        = %00000000

VAR
  long MemDisp[_screensize]     'OLED display driver variables 
  long MemWork[_screensize]     'graphics driver variables  

OBJ
  OLED          : "OLED-Driver1"
  Graphics      : "OLED-Driver2"
  midiIn        : "XBee_In2"
  midiOut       : "XBee_Out"

PUB main | dummy, i[3], num, d, x, y, color, x0, y0, x1, y1, x_0, y_0, x_1, y_1, c_x, c_y, r
  OLED.start(@MemDisp)
  Graphics.setup(_xtiles, _ytiles, @MemWork)
  midiIn.start(21)
  midiOut.start(20)
  num := 0
  repeat
    i[0] := cnt & $8000000
    if i[0] <> i[1]
      i[1] := i[0]
      num := ++num & 127
      dummy := $C00000 + num
      midiOut.fifoset(dummy)
    dummy := midiIn.event
    if dummy <> -1
      d := (dummy & $FF0000) >> 16
      if d == $FF
        Graphics.clear
        Graphics.copy(@MemDisp)
      elseif d < $E0
        x := d & $7F
        d := (dummy & $007F00) >> 8
        y := d & $3F
        color := d & $40
        d := dummy & $00007F
        color := color + d
        Graphics.plotPixel(x, y, color)
        Graphics.copy(@MemDisp)
      elseif d == $E0
        color := dummy & $00007F
        d := (dummy & $000100) >> 1
        color := color + d
      elseif d == $E1
        x0 := (dummy & $007F00) >> 8
        y0 := dummy & $00003F
      elseif d == $E2
        x1 := (dummy & $007F00) >> 8
        y1 := dummy & $00003F
        Graphics.plotLine(x0, y0, x1, y1, color)
        Graphics.copy(@MemDisp)
        x0 := x1
        y0 := y1
      elseif d == $E3
        x1 := (dummy & $007F00) >> 8
        y1 := dummy & $00003F
        Graphics.plotLine(x0, y0, x1, y1, color)
        Graphics.copy(@MemDisp)
      elseif d == $E4
        x_0 := (dummy & $007F00) >> 8
        y_0 := dummy & $00003F
      elseif d == $E5
        x_1 := (dummy & $007F00) >> 8
        y_1 := dummy & $00003F
        Graphics.plotLine(x_0, y_0, x_1, y_0, color)
        Graphics.plotLine(x_0, y_0, x_0, y_1, color)
        Graphics.plotLine(x_1, y_0, x_1, y_1, color)
        Graphics.plotLine(x_0, y_1, x_1, y_1, color)
        Graphics.copy(@MemDisp)
      elseif d == $E6
        x_1 := (dummy & $007F00) >> 8
        y_1 := dummy & $00003F
        y := y_1 - y_0
        repeat while y > 0
          Graphics.plotLine(x_0, y_0+y, x_1, y_0+y, color)
          y--
        Graphics.copy(@MemDisp)
      elseif (d == $E7) OR (d == $EF)
        c_x := (dummy & $007F00) >> 8
        c_y := dummy & $00003F
      elseif d == $E8
        r := (dummy & $007F00) >> 8
        Graphics.plotCircle(c_x, c_y, r, color)
        Graphics.copy(@MemDisp)
      elseif (d == $E9) OR (d == $F1)
        r := (dummy & $007F00) >> 8
      elseif d == $EA
        c_x := (dummy & $007F00) >> 8
        c_y := dummy & $00003F
        Graphics.plotCircle(c_x, c_y, r, color)
        Graphics.copy(@MemDisp)
      elseif d == $F0
        r := (dummy & $007F00) >> 8
        repeat while r > 0
          Graphics.plotCircle(c_x, c_y, r, color)
          r--
        Graphics.copy(@MemDisp)
      elseif d == $F2
        c_x := (dummy & $007F00) >> 8
        c_y := dummy & $00003F
        repeat while r > 0
          Graphics.plotCircle(c_x, c_y, r, color)
          r--
        Graphics.copy(@MemDisp)
PRI pauseMSec(Duration)
  waitcnt(((clkfreq / 1_000 * Duration - 3932) #> 381) + cnt)

→ 続きはこちら

2012年9月18日(火)

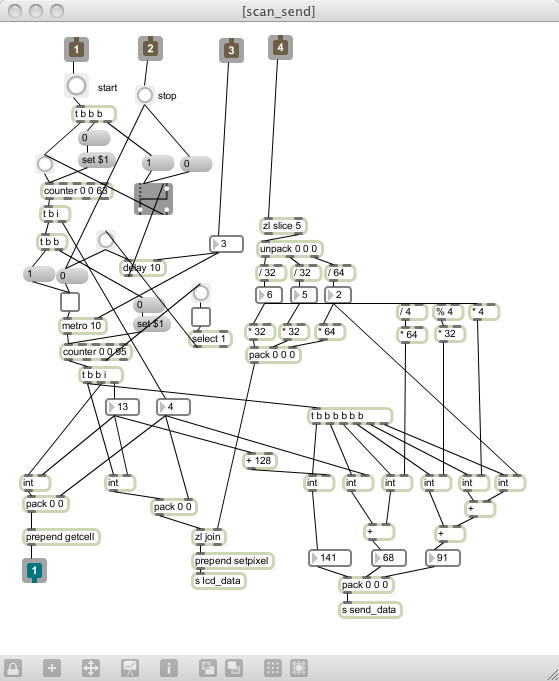
連休が明けて、いよいよお仕事モードが本格化してきた。 CGクリエイター検定の受験案内を掲示して、学会関係の連絡をやりとりして、 さらに特別研究に関する調査を始めたら、もう半日が経過した。 どうやら、ある部分は「Propeller」でもある、新しいターゲットが見えてきて、 デスクトップは遂に2台のパソコン3画面がフル稼働である。(^_^;)

「Propeller日記」というよりは「P板CAD日記」とでも言えそうな内容であるが、 しかしPropellerもダブル(かトリプル)で関係するので、このまま勢いでここに書いていこう。 要するに、汎用実験基板を新しく設計試作する、という事である。 これまで手ハンダを愛好してきた身としては、遠い昔のLSI設計以来の回路設計、 そして初めての基板設計、と新しい内容が盛りだくさん過ぎて死にそうである。 何より、仕事がWindows上、というのが最悪である(^_^;)。 しかしここを乗り越えれば楽しい事が待っている筈なので、ここは頑張っていこう。 Propellerについても、新しいアプローチが期待できる。 予告編の意味で、ここで関連する登場人物(候補)を並べてくと、以下のあたりである。


Propellerチップ


Propellerクイックスタートボード


PropStick USB


AKI-H8


Arduino Nano


Arduino　Mini


Arduino　Pro Mini


Gainer mini


XBeeモジュール

なにやらもの凄いことになっているが(^_^;)、本当はここに、以下も加えたいのをグッと堪えているのである。


Raspberry Pi


Propeller GCCボード

さて、ここからCAD地獄に突入する前に、昨日の最後に気付いたバグだけでも修正しておきたい。 本当は、Maxの側のバグを修正した上で、残り4種類8コマンドの「中心座標」「半径」「カラー」指定による「円」の描画、 までを完成したいところである。 今週末の日本音楽即興学会大会(神戸大学)でのプレゼンも作らなくてはいけないが(^_^;)。

しばらくMaxのパッチを掘り下げてみて、これまで「スキャン→転送」のモニタjit.pwindowと、 「生成→転送」のモニタjit.pwindowの二つがあった部分を改良して、 共通の「転送されるデータ」のモニタjit.pwindowにまとめた。 一部、スキャン転送処理のサブパッチ内の無駄な「send」「receive」変数を削除したところ、 これまで最高で4msecだったスキャン周期が3msecでもノイズが無くなった。 以下のように、画素スキャンした上に、さらに描画コマンドで重ね塗りすることが出来るようになり、 これで準備がようやく出揃った。

・・・しかし、ここでタイムアップである(^_^;)。 色々なお仕事とともに行う作業には制約もあるが、まぁ、あとは2-3時間程度あれば(そして忘れるほど時間が経過しなければ)、 この部分はほぼ機械的にやっつけられる、という状況である。 また、うまく時間が作れたときに遊ぶことにしよう。今日はここまで。

→ 続きはこちら

2012年9月19日(水)

朝、出かける間際に「めざましテレビ」でチラッと聞いた凄いニュースで、Propellerどころか、この日は午後まで、他に何も出来なかった。 Nature電子版 のニュースだと、以下のようなカンジである。
Proof claimed for deep connection between primes

If it is true, a solution to the abc conjecture about whole numbers would be an ‘astounding’ achievement.

10 September 2012

The usually quiet world of mathematics is abuzz with a claim that one of the most important problems in number theory has been solved.

Mathematician Shinichi Mochizuki of Kyoto University in Japan has released a 500-page proof of the abc conjecture, which proposes a relationship between whole numbers ― a 'Diophantine' problem.

The abc conjecture, proposed independently by David Masser and Joseph Oesterle in 1985, might not be as familiar to the wider world as Fermat’s Last Theorem, but in some ways it is more significant. “The abc conjecture, if proved true, at one stroke solves many famous Diophantine problems, including Fermat's Last Theorem,” says Dorian Goldfeld, a mathematician at Columbia University in New York. “If Mochizuki’s proof is correct, it will be one of the most astounding achievements of mathematics of the twenty-first century.”

Like Fermat’s theorem, the abc conjecture refers to equations of the form a+b=c. It involves the concept of a square-free number: one that cannot be divided by the square of any number. Fifteen and 17 are square free-numbers, but 16 and 18 ― being divisible by 42 and 32, respectively ― are not.

The 'square-free' part of a number n, sqp(n), is the largest square-free number that can be formed by multiplying the factors of n that are prime numbers. For instance, sqp(18)=2×3=6.

If you’ve got that, then you should get the abc conjecture. It concerns a property of the product of the three integers axbxc, or abc ― or more specifically, of the square-free part of this product, which involves their distinct prime factors. It states that for integers a+b=c, the ratio of sqp(abc)r/c always has some minimum value greater than zero for any value of r greater than 1. For example, if a=3 and b=125, so that c=128, then sqp(abc)=30 and sqp(abc)2/c = 900/128. In this case, in which r=2, sqp(abc)r/c is nearly always greater than 1, and always greater than zero.

Deep connection

It turns out that this conjecture encapsulates many other Diophantine problems, including Fermat’s Last Theorem (which states that an+bn=cn has no integer solutions if n>2). Like many Diophantine problems, it is all about the relationships between prime numbers. According to Brian Conrad of Stanford University in California, “it encodes a deep connection between the prime factors of a, b and a+b”.

Many mathematicians have expended a great deal of effort trying to prove the conjecture. In 2007, French mathematician Lucien Szpiro, whose work in 1978 led to the abc conjecture in the first place claimed to have a proof of it, but it was soon found to be flawed.

Like Szpiro, and also like British mathematician Andrew Wiles, who proved Fermat’s Last Theorem in 1994, Mochizuki has attacked the problem using the theory of elliptic curves ― the smooth curves generated by algebraic relationships of the sort y2=x3+ax+b.

There, however, the relationship of Mochizuki’s work to previous efforts stops. He has developed techniques that very few other mathematicians fully understand and that invoke new mathematical ‘objects’ ― abstract entities analogous to more familiar examples such as geometric objects, sets, permutations, topologies and matrices. “At this point, he is probably the only one that knows it all,” says Goldfeld.

Conrad says that the work “uses a huge number of insights that are going to take a long time to be digested by the community”. The proof is spread across four long papers1-4, each of which rests on earlier long papers. “It can require a huge investment of time to understand a long and sophisticated proof, so the willingness by others to do this rests not only on the importance of the announcement but also on the track record of the authors,” Conrad explains.

Mochizuki’s track record certainly makes the effort worthwhile. “He has proved extremely deep theorems in the past, and is very thorough in his writing, so that provides a lot of confidence,” says Conrad. And he adds that the pay-off would be more than a matter of simply verifying the claim. “The exciting aspect is not just that the conjecture may have now been solved, but that the techniques and insights he must have had to introduce should be very powerful tools for solving future problems in number theory.”

この「ABC予想」の証明が正しければ、なんとあの「フェルマー予想」の証明が即カンタンだ、というのだから聞き捨てならない。 今度は ABC予想 を調べてみると、以下のようなカンジであり、既にこの京大の望月先生の証明のニュースが加筆されていた。
ABC conjecture

A remarkable conjecture, first put forward in 1980 by Joseph Oesterle of the University of Paris and David Masser of the Mathematics Institute of the University of Basel in Switzerland, which is now considered one of the most important unsolved problems in number theory (but see the section below this introduction). If it were proved correct, the proofs of many other famous conjectures and theorems would follow immediately - in some cases in just a few lines. The vastly complex current proof of Fermat's last theorem, for example, would reduce to less than a page of mathematical reasoning. The ABC conjecture is disarmingly simple compared to most of the deep questions in number theory and, moreover, turns out to be equivalent to all the main problems that involve Diophantine equations (equations with integer coefficients and integer solutions).

Only a couple of concepts need to be understood to grasp the ABC conjecture. A square-free number is an integer that isn't divisible by the square of any number. For example, 15 and 17 are square-free, but 16 (divisible by 42) and 18 (divisible by 32) are not. The square-free part of an integer n, denoted sqp(n), is the largest square-free number that can be formed by multiplying the prime factors of n. Thus, for n = 15, the prime factors are 5 and 3, and 3 × 5 = 15, a square-free number. So sqp(15) = 15. On the other hand, for n = 16, the prime factors are all 2, which means that sqp(16) = 2. Similarly, sqp(17) = 17 and sqp(18) = 6. In general, if n is square-free, the square-free part of n is just n; otherwise, sqp(n) represents what is left over after all the factors that create a square have been eliminated. In other words, sqp(n) is the product of the distinct prime numbers that divide n. For example, sqp(9) = sqp(3 × 3) = 3 and sqp(1400) = sqp(2 × 2 × 2 × 5 × 5 × 7) = 2 × 5 × 7 = 70.

The ABC conjecture deals with pairs of numbers that have no common factors. Suppose A and B are two such numbers and that C is their sum. For example, if A = 3 and B = 7, then C = 3 + 7 = 10. Now, consider the square-free part of the product A × B × C: sqp(ABC) = sqp(3 × 7 × 10) = 210. For most choices of A and B, sqp(ABC) is greater than C, as in the example above. In other words, sqp(ABC)/C > 1. Occasionally, however, this isn't true. For instance, if A =1 and B = 8, then C = 1 + 8 = 9, sqp(ABC) = sqp(1 × 8 × 9) = sqp(1 × 2 × 2 × 2 × 3 × 3) = 1 × 2 × 3 = 6, and sqp(ABC)/C = 6/9 = 2/3. Similarly, if A = 3 and B = 125, the ratio is 15/64, and if A = 1 and B = 512, the ratio is 2/9.

David Masser proved that the ratio sqp(ABC)/C can get arbitrarily small. In other words, given any number greater than zero, no matter how small, it's possible to find integers A and B for which sqp(ABC)/C is smaller than this number. In contrast, the ABC conjecture states that [sqp(ABC)]n/C does reach a minimum value if n is any number greater than 1 - even a number such as 1.0000000000001, which is just barely larger than 1. The tiny change in the expression makes a vast difference in its mathematical behavior. The ABC conjecture in effect translates an infinite number of Diophantine equations (including the equation of Fermat's last theorem) into a single mathematical statement.

The ABC Conjecture proved?

In 2012, Shin Mochizuki claimed to have proved the ABC Conjecture using a new set of techniques, which he calls “inter-universal geometry” - a generalization of the foundations of algebraic geometry. In a nutshell, Mochizuki has devised a new scheme of mathematical objects, which he believes he understands well enough to apply to proving this long-standing problem in Diophantine analysis.

It will take some time for other mathematicians to check through Mochizuki's proof because first they will have to make themselves familiar with the world of inter-universal geometry. But Mochizuki reputation is sufficiently high, and the Conjecture sufficiently important, that the effort will be made.

そして、ニュースのリンクに従って 宇宙際幾何学者・望月新一 というページ(「宇宙際」というのは「国際」など小さなものでは無い、という事かぁ!?)に行ってみると、 太っ腹に、この証明の論文(4分割されていて総計500ページ!)のPDFが置かれていた。 ニュースで集中しているらしく京大のサーバでも切れ切れだったが(^_^;)、ゲットした。これである。 ★ ★ ★ ★

これは査読に相当な時間がかかるだろう、という事だけ判った(^_^;)。 「宇宙際」というのは、過去にuniversalがあるのを拡張してinter-universalと呼んだようである。 2ちゃんねるで、以下のようにスッキリと整理して解説した人は、相当に解っている人だろう。 

==予備知識==
abc-triple
	正の整数 a,b,c について、a + b = c かつ a, b は互いに素である三つ組 (a, b, c)
rad(n)
	正の整数 n の、素因数の積。
		(例) rad(504) = rad(2^3 * 3^2 * 7) = 2 * 3 * 7 = 42
		504の素因数は、2と3と7だからrad(504) = 2*3*7 =　42

==abc予想==
任意の abc-triple は、c ＜ {rad(abc)}^2 を満たす。

==Oesterle, Masserによる一般化==
abc-triple は（有限個の例外を除き一般に）、c ＜ rad(abc)^κ を満たす（κ は1以上の実数）
(κは1.62991より大きい)

==abc予想からフェルマーの定理の証明==
a=x^n, b=y^n, c=z^n が互いに素でa+b=cを満たしているなら
z^n=c ＜ rad(x^n y^n z^n)^2 =　rad(xyz)^2 ＜ (xyz)^2 ＜ z^6
よって n＜6 である。
n=3,4,5のときは証明済みだからフェルマーの定理が成り立つ。
大学時代、同じ京大理学部でも、数学に進む同級生は、一般の我々が一晩かかって解くような問題をチラッと見ただけで「こうちゃう?」と解いていたので、 まぁ、数学者というのは別次元である、というのは知っている。 僕は数学をやりたくて京大に行ったのだが、キッパリ諦めるのに入学して1ヶ月かからなかった(^_^;)。 物理屋とか電気屋は頑張ればなれるが(物理屋は理論や道具から作るところが違い)、数学屋は別なのだった。 それで僕は音楽屋と並行して、物理屋から電気屋/情報屋になったのであった。 論文PDFはどこを眺めても判らないが、まぁ、お宝である。いずれこれをスマートに解説してくれる本が出るのを待つことにしよう。

そういえば、過去に湯川秀樹先生のノーベル賞論文の原本と手書きの原稿が京大から復刻PDF公開された時にゲットした事があった (僕の出身研究室の遠い先輩に「朝永振一郎」「湯川秀樹」がいる、というのは事実)。 これである。 ★ ★
ここまで来ると物理とは言っても数学か哲学か、という世界である。 Propellerとかコンピュータアルゴリズムの解りやすい世界でヨカッタ、というべきなのか。 もっとも、音楽の世界は、このような言語による記述すら許さないのだから、もっと深いのかもしれない(^_^;)。

午後には、毎月のお楽しみとなり始めたが、1回生の金重さんが研究室にやってきて、先月の 「飛ぶドラえもん」 に続いて、 「風で光るドラえもん」 を作って、それぞれYouTubeに動画を上げた。 定期購読のシールを送ると、さらに「飛ぶのび太くん」が来るらしい。(^_^)

そして放課後には、OGの野口さんが、来月冒頭に予定している 個展 の打合わせに来るために、裏でずっとポスターを印刷している。 また一方で、Webサーバのメンテナンスをしようとsshしてみるとタイムアウトで、 問い合わせたところSUAC情報室が勝手に教員棟からのsshポートを閉じていたと判明、 あり得ないので至急対応して・・・などとドタバタしているうちに、この日は終わるのであった(^_^;)。 「(Propellerも載る)基板CAD日記」にも入れなかったが、果たして今後の展開やいかに。

2012年9月20日(木)

ネットでは昨日の望月教授の「ABC予想を証明」というニュースの余韻がまだ続いている。 計500ページを超える4本の論文PDFを京大のサーバからダウンロードしたものの、 関連解説資料などを計100ページほど印刷しただけで、論文そのものは塩漬けしておくつもりだったが、 せっかくなので、お仕事の傍らで打ち出すことにした。 プリンタはたぶん、今日ずっと唸っているだろう。A4用紙が1袋(500枚)、消えることになる(^_^;)。 今日は午後の教授会だけで他に予定もなく(夕方に学生が来るアポだけ)、 こちらはごく世俗的に、地味に遅々として、「初めての基板CAD」に挑戦してみよう。

SUAC事務局にも了解を得て、今回の基板は「 P板.com 」という会社で作る予定である。 この会社は、2年前の大垣での MOM2010 の時にブースを見てナルホドと気になっていた会社で、名刺ももらっていた。 この2年間のSketchingブームで、だいぶ躍進している模様である。 回路設計/基板設計を依頼するほどの予算が無いので、自分でやってみよう(^_^;)、 というのが、今回のチャレンジである。 Propellerは中心に据えるつもりなので、引き続きこの「続・Propeller日記」にメモしつつ進めていこう。

今回の基板を「 P板.com 」で作ろうと思った理由は、大学研究室レベルの実験試作に機動的に対応しているらしいこと、 値段もほぼ一番安いことだけでなく、Windows上ではあるものの、

という、相互に連携した設計支援ツールを無料で提供/サポートしているからである。 3番目のものはともかく、それほど複雑巨大でもない今回の基板については、ちょうど「身の丈」であり、 わざわざ高価なCADソフトを買うつもりは無いので、最適というわけである。

今回の基板は、「各種マイコン共用の汎用I/Oボード」である。 これまで、新しいシステム(楽器/インターフェース/インスタレーション)ごとに、 ホストマイコンを選び、ほぼ定番のI/Oを個別に組んできたが、 Sketchingをより一般化させたいので、「共用の汎用I/Oボード」を作りたいのである。 Gainer小林さんが流行らせたように、確かにブレッドボードは簡単であるが、 あまりに実際の作品に対して信頼性が無さ過ぎて、僕は無理である。 ハンダ付けは必須であり、ブレッドボードで最終的な作品まで作ってOK、という人達が信じられない(^_^;)。

ブロック図を手描きするまでもないので、ここで、これまであれこれ脳内で検討してきた仕様を以下に整理しておこう。 まだ思いついたりする事もあるのでブランクも残し、これは後日、刻々と追加/変更していく可能性がある。 基板サイズについては、「汎用」なので、無理に小さくする必要はない、というスタンスである。

  • 基板上に複数のマイコンボードのパターンを搭載する。ただし同時に実装するのは必ず1つだけ
  • 搭載マイコンとしてPropStickUSBに対応する
  • 搭載マイコンとしてAKI-H8に対応する
  • 搭載マイコンとしてArduino Nanoに対応する
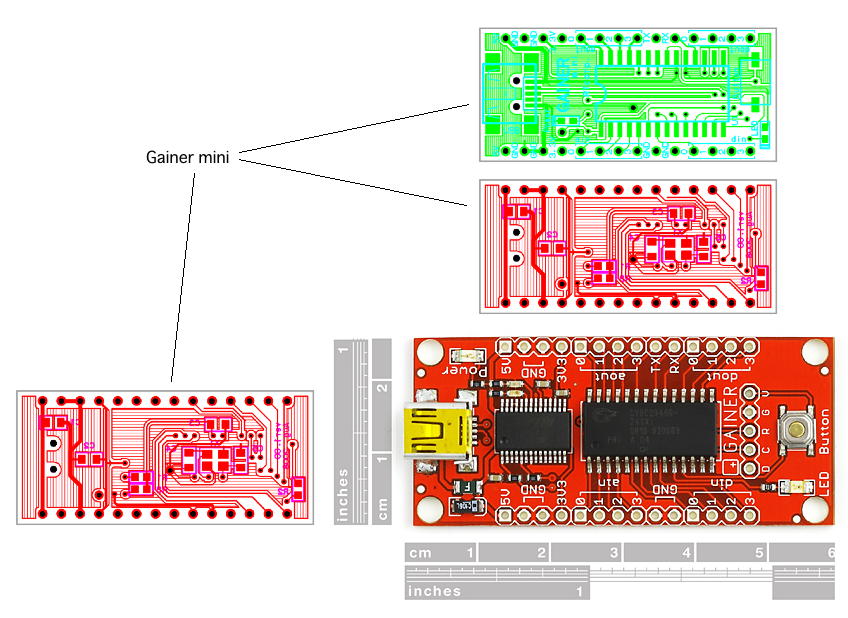
  • 搭載マイコンとしてGainer miniに対応する
  • 他に「XBeeゲタ基板」(0.1インチ間隔に変換する秋月電子の基板)に対応する
  • 電源は要検討(+5V系、+3.3V系、+6V以上入力)★
  • 基板上の信号レベルは基本的には「+5V系」として個別に対応
  • マイコンへの書き込みはそれぞれのボード上のミニUSBコネクタで対応(AKI-H8はライタへの専用コネクタ)
  • MIDI入出力を完備する(Gainer以外。Arduinoは送信のみ)
  • Gainerのモードは要検討★
  • ディジタル出力は共用8ビットバスを8個の74HC574に配して「64ビット同時出力」に対応
  • ディジタル入力は共用8ビットバスに8個の74HC245から受けて「64ビット同時入力」に対応
  • 電流ドライバ(LED/モーター/ソレノイド/リレー)は搭載しない
  • アナログ入力は複数ビット対応マイコンは各自直結、他に汎用A/Dに8チャンネルのマルチプレクサ入力を検討★
  • アナログ出力はPWM対応マイコンは各自直結、他に汎用D/Aに8チャンネルのS/H出力を検討★
  • 外部インターフェースのコネクタは秋月電子の2列ピンヘッダ
  • Propellerチップ(+周辺回路)は今回は搭載しない
  • PropQuickStartは実験だけで今回は搭載しない
  • Arduino Miniは実験だけで今回は搭載しない
  • Arduino Pro Miniは実験だけで今回は搭載しない
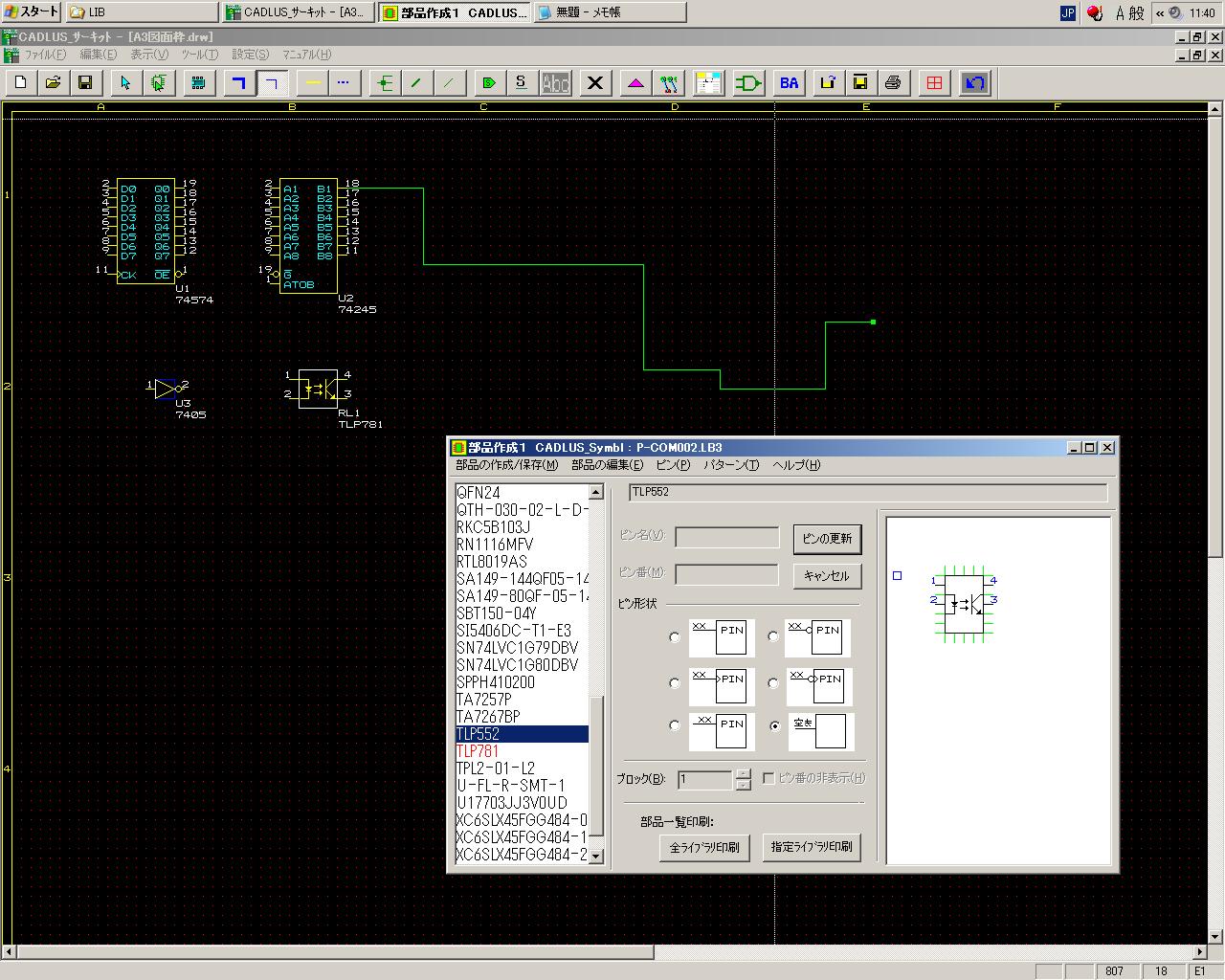
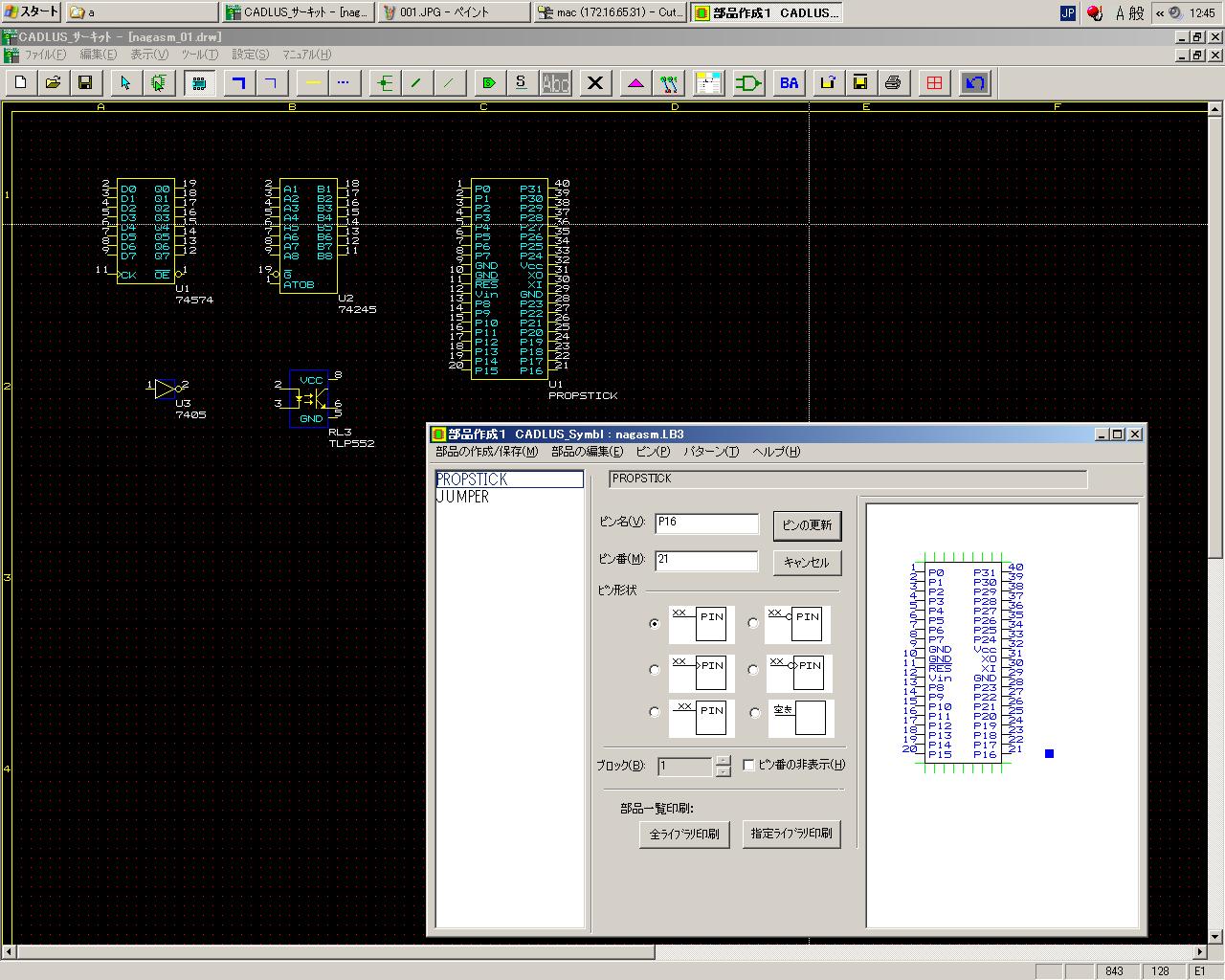
さて、さっそくとりあえず、「初めての回路設計CAD」である。 9月18日の写真にもチラッと写っていたが、 回路設計CAD CADLUS Circuit を起動して、とりあえずはコネクタとかジャンパから「部品」として登録してみて、操作方法を調べてみることにする。 まずは、回路設計CADとパターン設計CADに関して、ダウンロードしたツールに付属していたマニュアル3本 を、いちいちオンラインで引くのも面倒なので、全てプリントした。 やはり、マニュアルは「紙」が一番である(^_^;)。 そして、とりあえず以下のように触ってみたが・・・こりゃあ大変だ。 予想していたことだが、まったく使いにくい。CADの人たちは、これに馴れていくのかぁ。(^_^;)

上にあったように、TTLの74HC574とか74HC245とか74HC05などはそのまま使えるし、 ジャンパやコネクタも完備していた。 初めて知ったが、回路設計CADでは論理的な「部品」を定義するものの、 実際のその部品の外形に合わせたピン位置などは、どうもパターン設計CADの方で登録するらしい。 ということは、フォトカプラとか各マイコンボードなど、ライブラリに無い部品をまず、 新しい部品として登録してライブラリに加える、という作業から始めることになりそうだ。

・・・そして昼休みをまたいで、ようやく以下のように、フォトカプラTLP552と、 Propellerスティックボード を、シンボルとして登録できた。これはあくまで仮想的なシンボルでしかない。 いやー、こりゃ長い道のりだ。

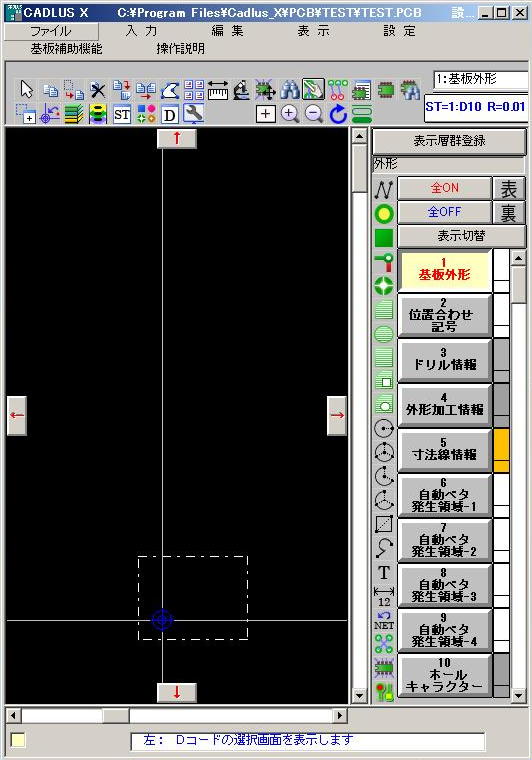
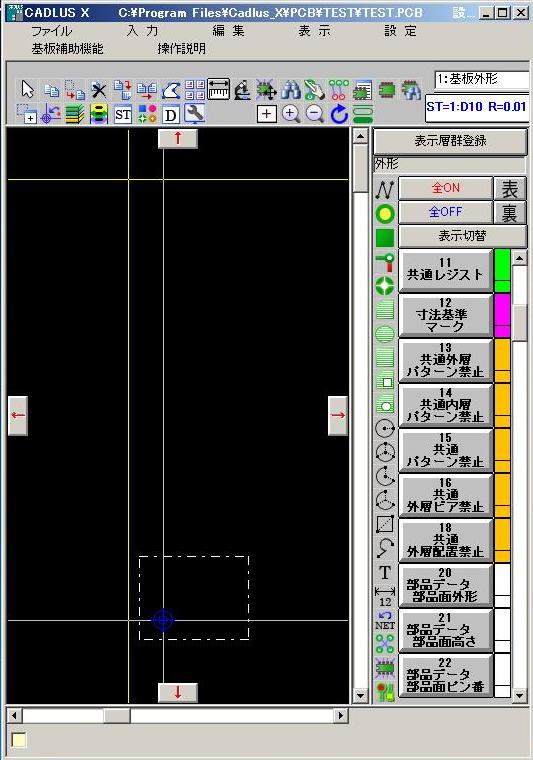
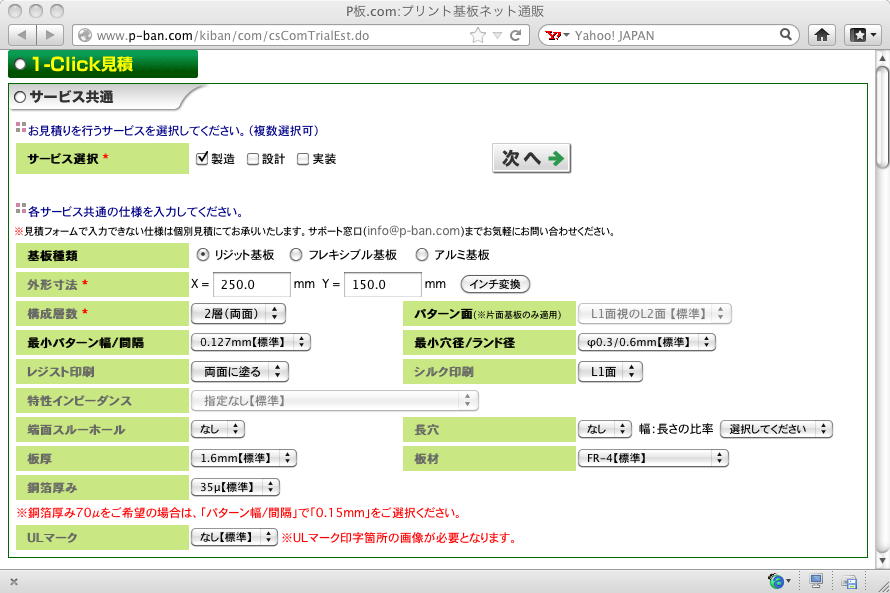
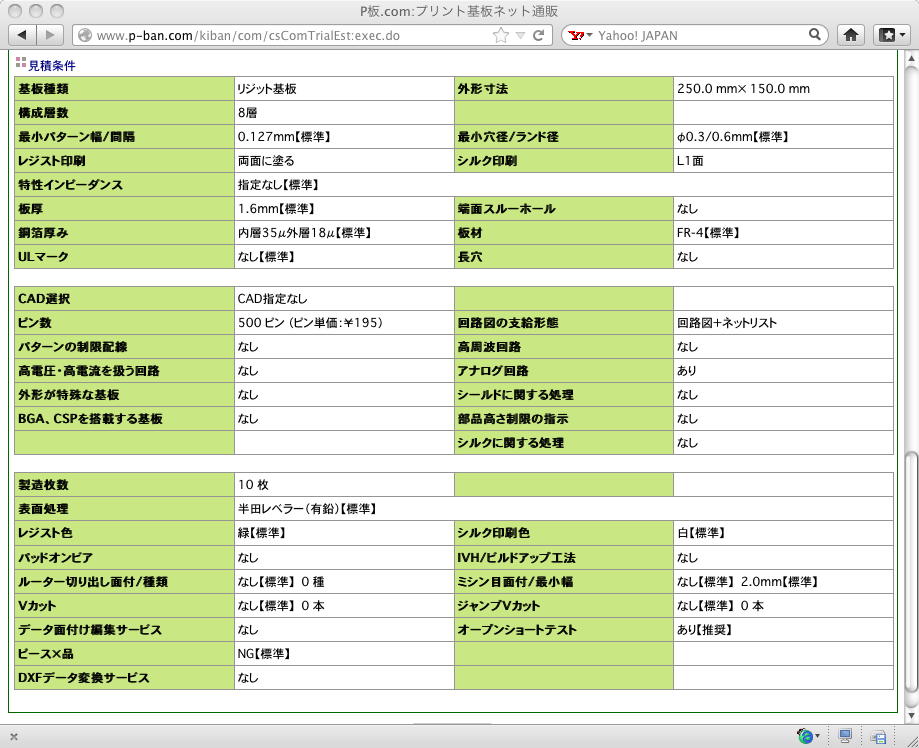
とりあえず作業の全体像を知りたい、ということで、次に パターン設計CAD CADLUS X を起動してみたが、なんだかこれはもの凄いことになっている(^_^;)。 いろいろやってみたが、まったく判らない。 だいたい、1枚の基板のパターン設計のためには、以下のように、もの凄い階層のそれぞれに必要な設計を行う必要があり、 これはつまり、部品ごとの「実際の外形やピン配置」の登録についても、この多くに対応して設計登録する必要がある、 という事である。 これは第一印象として「無理」である。 あくまで回路図設計データ(部品登録とネットリスト)までで、基板設計は委託するしかないのでは・・・という確かな確信が。(^_^;)

心が折れそうになりながら(^_^;)、 P板.com にある「1-Click見積り」というページで調べてみることにした。 ここでは「製造サービス(実際の基板試作)」、「設計サービス(基板のCAD設計)」、「実装サービス」の3カテゴリがある。 考えている実験基板では、チップ部品などの特殊なものは無く、全て0.1インチの穴で簡単にハンダ付けできる、 難易度は「電子工作キット」程度なので、3番目の「実装サービス」は不要である。 そこで以下のように、まず「共通事項」を仮想的に入力した。 サイズを「250mm×150mm」としたのは、「2層(両面)」としたからである。 これは後で、「200mm×100mm」で「4層(両面)」ならどうなるか、比較してみたい。

そして引き続き、以下のように「設計事項」を入れてみた。 ピン数の「500」というのがまったく適当であるが(^_^;)、これも「1000」としてどうなるか、比較してみよう。

この結果、出て来た「設計サービス」の見積り(税込み)は、 このように なって、133,875円であった。そのままピン数を「1000」としてみると、 このように なって、236,250円とほぼ倍増した。 やはり、目安である「ピンあたり130円」がそのまま反映されているようだ。 そして、再びピン数を500ピンに戻して、今度は「200mm×100mm」で「4層(両面)」としてみると、なんと このようになり、 まったく同額の133,875円であった。それなら4層(電源とGNDを内部層にするとノイズ耐性が大きく向上)の方がいいに決まっている。 なんとこれは、6層にしても8層にしても、そして基板サイズを「250mm×150mm」としても同じであった(^_^;)。 つまり設計コストでなく、「層」と「サイズ」は製造コストに影響するらしい。

次に、共通である「設計サービス」に加えて、基板試作の「製造サービス」までの合計というのを、 まずは以下のように、「500ピン」「250mm×150mm」「8層」という条件で、 「10枚」(イニシャルコストの必要なリピートでなく単発の試作)として求めてみると、 このように 242,350円(うち設計が127500円)となった。 特急試作とかの割り増しは不要なので、一番安い「ノーマル」指定である。

そして、条件をそのまま「2層(両面)」とすると、 このように 165,543円(うち設計が127500円)となった。 やはり2層と8層では、10枚試作の製造コストが3万円と10万円、という違いになっていた。 そこで最後に「4層」としてみると、 このように 税込みで185,262円となった。10枚試作の製造コストは5万円である。

これは、想定していた試作予算としては、まずOKである。 基板サイズを「200mm×100mm」にしても177,093円だったので、 実際にはピン数が最大のファクターとなりそうだが、回路設計のみで行けそうである。

そして最後に、「500ピン」「250mm×150mm」「4層」、 さらに「回路図の支給形態」を「回路図+ネットリスト」でなく「回路図のみ」としてみたのが これ である。 税込みで201,012円。ネットリストへの変換まで任せるということは、 「回路設計CAD CADLUS Circuit」で、部品の登録と、それらのピン番号までを対応付けた回路設計だけでいい(信号を結ぶ配線作業ナシ)、 という事だろう。これは確認するとして、もう決まりである(^_^)。 何のことはない、「基板設計CADナシ」で行けるのであった。 もしかして「回路図のみ」の場合には、手描きの回路図と部品資料だけでもいいのかなぁ。(^_^;)

2012年9月21日(金)

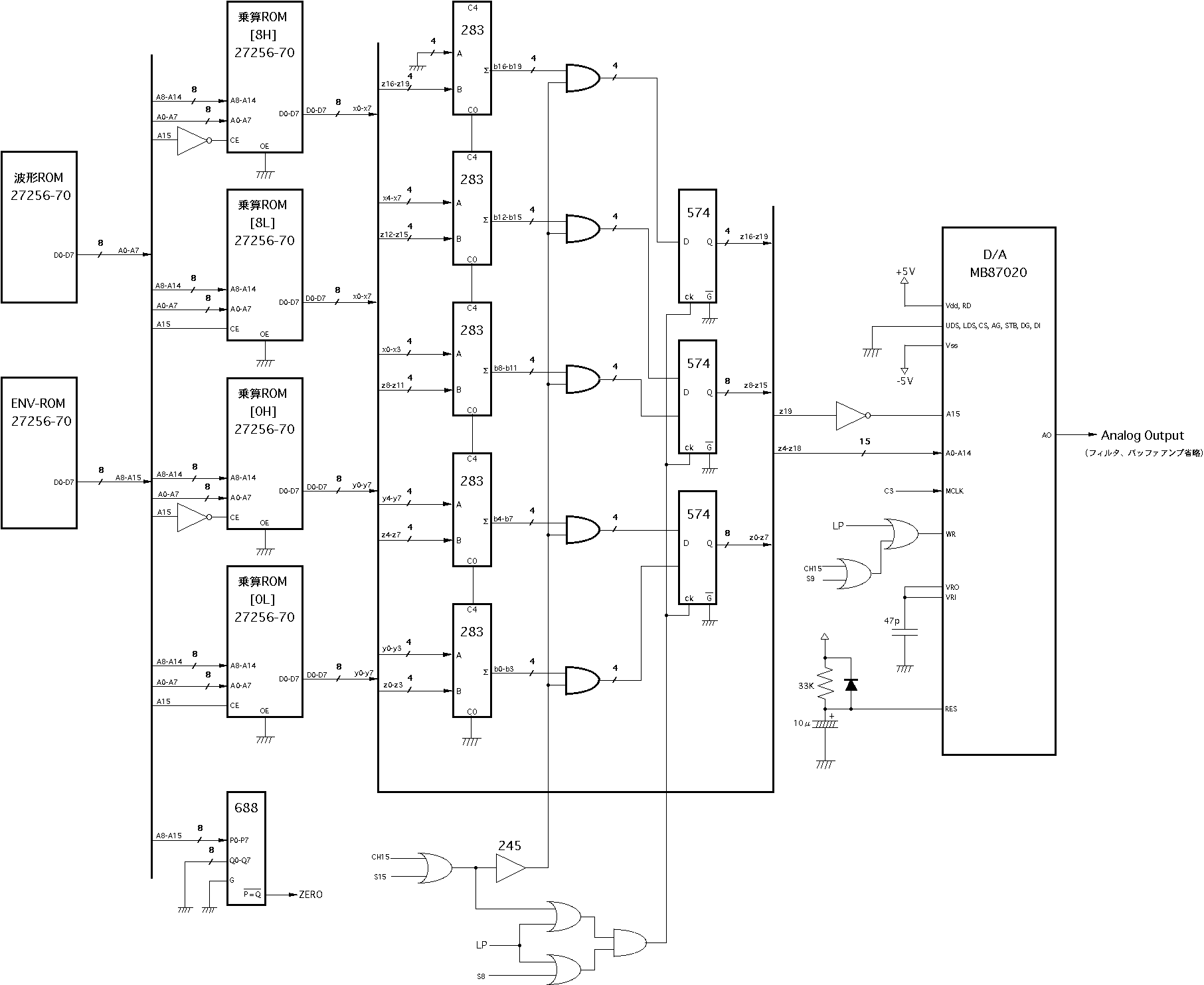
午前に外出予定があり、明日からの音楽即興学会出張の準備とかも色々あって、あまり進めない日と判っていたが、 朝、研究室に来てみると、 P板.com から、昨日の質問に対する回答が以下のように届いていた。さすがである(^_^)。 
長嶋 洋一 様

いつもお世話になっております。P板.comサポート窓口 ○です。 
お問い合わせいただきまして、誠にありがとうございます。 

> 質問(1)ネットリストというのは、「CADLUSCircuit」でエラーが出なくなるまで
> 設計が完了すれば自動で生成されるのでしょうか。 

いいえ、ネットリストの出力はツールアイコンの「CADLUSネット出力」かメニューの
ファイルの「CADLUSネット出力」で出力先フォルダとファイル名を指定して出力します。
拡張子がnetはCADLUS Xのバイナリーデータで、拡張子がnxtはアスキーデータです。
どちらでも結構です。
xxxxxx.net
xxxxxx.nxt

> 質問(2)「回路図のみ」というのは、手描きの回路図と各部品のデータシート
> だけでもいいのでしょうか。 

手描きの回路図と各部品のデータシートだけで結構でございます。

以上、宜しくお願いいたします。
素晴らしい。簡潔にして明瞭である(^_^)。 これまで過去には、1999年に発表した 作るサウンドエレクトロニクス では、

というブロック図を設計して、具体的な回路図としては以下の3枚にわたる規模となり

実際の製作ではプリント基板など起こさず、手ハンダによって、以下のように製作して稼働させたことがあった。

また過去には、2008年に発表した 電子十二影坊 (Dodeca Propeller) では、13個のPropellerを搭載したシステムを製作した。 回路図と手ハンダで製作した基板の様子は以下である。

これらに比べれば、今回の基板なんて可愛いものである。 今までのようにドローソフトで回路図を作るのもいいが、せっかくなので、諦めるまでは、 「CADLUSCircuit」できちんとCAD入力して、配線のエラーチェックを通すまでやってみたいと思う。 この週末は出張を挟むので、みちみち電車の中とか学会の内職(^_^;)で、 それぞれのマイコンボードの技術資料等を整理しておいて、実際に回路図にまとめるのは来週以降にしよう。

午後に半日の時間があったので、ここであらためて「基板」について整理してみた。 部品棚からは、これまで定期購読している「トランジスタ技術」「エレキジャック」等に付録として付いてきていた、 CQ出版の実験用基板がたくさん出て来た。 まったく作っていなかったが(^_^;)、せっかくなので、搭載予定のマイコンボードとともに以下のように机に並べてみた。

なかなか壮観である(^_^)。 そして、第1のグループとして、以下の「紙フェノール基板」(だと思う(^_^;))がある。 これは片面基板で、素材ももっとも安いもので、主としてアナログ基板に使われる。

続く第2のグループとしては、以下の「紙エポキシ基板」(だと思う(^_^;))がある。 これも片面基板であり、素材としてやや高価になるが、より細かいパターンが描画できるようだ。 こちらもアナログ主流のようだが、一部ディジタル回路もある。

以下の1枚だけは、ちょっと特殊で謎である(^_^;)。 少なくとも両面基板だが、パターンがよく見えないので安心できない。 4層というよりは、たぶんパターンをレジストで隠しているのだろうが、これでは切った貼ったの修正が困難である。

そしてここからが、今回の基板でもたぶん使う、以下の「ガラスエポキシ基板」(だと思う(^_^;))である。 これでもたぶん4層ではなくて両面基板で、ピン間は1本という、そこそこ大人しいものばかりである。

そしてなんと、アルテラのFPGAボードかな、遂に「P板.com」と書かれた基板を発見(^_^)。 これも同じで、たぶん両面、ピン間1本、そしてAKI-H8のコネクタと同じ0.1インチが2列というコネクタのパターンもあり、 おおいに参考になりそうである。

以下は、今回の実験試作基板に搭載予定(といっても同時にでなく、常にいずれか1枚を実装)のマイコン群とXBeeの下駄基板(秋月電子)である。 XBeeはなんとも高飛車に、ビン間隔が0.1インチ(2.54mm)でなく2ミリである。 この間隔を特殊に定義するよりも、基板は全てインチで指定する方が安全なので、秋月の下駄基板を標準とする。 この下駄基板はビン間隔の補正だけでなく、電源のレギュレータも載っているので便利なのである。

そして以下が、いつも実験でもシステム組み込みでも活用している、サンハヤトのユニバーサル基板である。 調べてみると、手前がサンハヤトの「ユニバーサル基板　ICB-96GU」で、仕様は「寸法 115×160mm」「材質・板厚 片面・ガラスコンポジット1.2t」 「仕上処理 ハンダ」「パターン 2.54mmピッチICパターン」「穴径0.9φ」とあった。 向こうのものはいつもマルツで10枚単位で袋買いするが、調べてみるとマザーツール社の「ユニバーサル基板　UP-201」であり、 仕様は「寸法 115×160mm」「材質 片面＝フェノール HB材 1.6t」「仕上処理 フラックス」「パターン 2.54mmピッチ ドット」「穴径φ1.0mm」とあった。 微妙に穴径が違っていたが、サイズと、四隅の取り付け穴の位置もぴったりである。

今回の基板は、実はこのサイズを狙っている。「ICB-96GU」「UP-201」と同一サイズにすることで、 この実験試作基板をさらに拡張する場合に、以下の過去の実例のように、これらユニバーサル基板とスタックできるのである。 これはとても有効である。

そこで以下のように、「UP-201」の上にマイコンを並べてみた。この残りスペースになんとか他の回路とコネクタを詰め込む作戦である。

上の写真には、Arduino Nanoの姿が見えない。 しかし実は、以下のように、AKI-H8の下に配置するつもりである(^_^;)。 同時に実装する事はないので、AKI-H8の下のスカスカのスペースが勿体ないので、 回路設計としては同時に存在するように設計するつもりで、それでOKかどうか、 さきほど昨日に引き続いて問い合わせのメイルを出してみたところである。

およその作戦はこんなところである。 昨日のオンライン見積りでは「250×150mm」としたが、「115×160mm」に入れば、 製造コストも多少は安くなるし、実際のシステムに内蔵する自由度が向上するので、 なんとかこのサイズを死守したいところである。 ・・・というところで、なんとP板.comサポートから、速攻で質問の回答メイルが届いた。 
静岡文化芸術大学 長嶋　洋一 様 

いつもお世話になっております。P板.comサポート窓口 ○○です。 
お問い合わせいただきまして、誠にありがとうございます。 

> (1)部品の下に部品を置いてもいいでしょうか 

充分なスペースがあるのであれば、特に問題ないかと思われます。

> (2)カット対応ジャンパはどのように? 
> が、ちょっと見つけられませんでした。 

「CADLUSCircuit」でジャンパー部品を登録する場合は通常の2足の抵抗部品と
同様に1番、2番と端子番号を付けて作成してください。
設計のご依頼時は穴径、ランド径、ピッチを設計仕様のコメントとして記述してください。
部品表はJ1,J2など部品参照名で分かりますので、適当でかまいません。

宜しくお願いいたします。
素晴らしい。またまた簡潔にして明瞭である(^_^)。 なるほど、どうやら細かいところは「設計仕様のコメント」で、 かなり柔軟に対応してくれそうである。 「適当でかまいません」には痺れた。お役所的でも権威主義でもない、ものづくりを応援する、いいカンジである。 これは、頑張って、ぜひとも「P板.comユーザ」の仲間入りを果たしたい、と思えてきた。

2012年9月22日(土)

そして例のごとく、移動中の名鉄特急ミュー車内である。 欧州ツアー で「乗り鉄」の血が蘇り、今回の往路は敢えて新幹線でなく、 「JR→名鉄→近鉄→阪神」で関西を目指す(^_^;)、というマニアックな出張である。

ネットに繋がっていないので車中で出来る事には限りがある。 未だに携帯電話を持たずPHSだけの僕だが、モバイルWiFiルータがあれば・・・と揺らいだ時期もあったが、 それほど出張も多くないので、このまま出張では「ホテルや会場ではWiFi」「駅ではPHSからダイヤルアップ」で不自由ない。 あくまで携帯機器ではメイルを打たない(僕がPHSで文字を打つのは電話番号登録の名前だけ)、という主義でいきたい。 世間のiPhone5の騒ぎはまったく無縁である。(^_^;)

ということで、ここではいずれ必要な作業の一部をサクサクと進めることにする。 せっかくの「Propeller日記」であり、ちょうど PropStickUSB のPDFが手元にあるので、これを最初の題材として、今回の実験試作基板に搭載するための設計情報の整理、 という作業に着手した。 今後、全ての搭載予定マイコンに対して、およそ共通に以下の確認作業が必要である。

  • 電源供給(+5Vか+3.3VかACアダプタ[5-9V]か)
  • リセット(負論理でSW経由でGNDショートでOK?)
  • 書き込み手法(オンボードコネクタ?)
  • ディジタル出力ポートの電圧(+5Vか+3.3Vか)
  • ディジタル出力ポートの電流ドライブ能力(LED直接ドライブの可否)
  • ディジタル入力ポートの電圧(+5Vか+3.3Vか)
  • ディジタル入出力ポートの総数
  • アナログ入力ポートの電圧(5Vか3.3Vか)
  • アナログ入力ポートの総数
  • アナログ出力に関して(PWM/電圧)
  • MIDI入力増設法
  • MIDI出力増設法
  • シリアル入出力増設の対応(→XBee接続)と信号電圧(+5Vか+3.3Vか)
  • ビンは定義されているが回路としては「NC」となる信号(回路設計CADの身配線エラー対策)
  • 総ピン数
  • 外形寸法、mil幅、ビン配置/定義の図面
このような条件に対して、 PropStickUSB などを参照して、個々にコメントしていくことで、実験試作基板の回路全体の設計が仕上がっていく、という作戦である。 さっそく、今後に共用できるように検討項目を薄くしたテンプレートを作って、PropStickUSBについて検討してみた。
  • PropStickUSB
  • ※1ピンはミニUSBコネクタとは反対側なので向きと位置に注意すること
  • このボードはPropellerチップの全機能をほぼ完全に提供しているので「Propellerチップ単体」搭載は不要
  • 搭載水晶は5MHzなので「16倍モード」で最大能力の80MHzがOK
  • 電源供給(+5Vか+3.3VかACアダプタ[5-9V]か)
    VIN端子(12ピン)に+5Vを供給するとオンボードレギュレータで内部+3.3Vを供給、 さらに+30℃の環境で280mAほど外部に供給できる。 VINが+9Vだと発熱のため100mAも無理なので、ACアダプタでなく+5Vとしたい
  • リセット(負論理でSW経由でGNDショートでOK?)
    GNDへのショートでOK。オンボードのResetスイッチあり(GNDとショートする)
  • 書き込み手法(オンボードコネクタ?)
    ボード上のミニUSBコネクタでそのまま書き込みOK(FTDI interfaceとインジケータLED搭載)
  • ディジタル出力ポートの電圧(+5Vか+3.3Vか)
    +3.3V系。+5V系への拡張用には74HC574でラッチ/74HC245でドライブ、または2SC1815で反転出力(+9VもOK?)
  • ディジタル出力ポートの電流ドライブ能力(LED直接ドライブの可否)
    Propellerチップと直結している。Propellerのデータシートから、各ポートごとに+3.3Vで40mA
  • ディジタル入力ポートの電圧(+5Vか+3.3Vか)
    +3.3V系、CMOSなのでその1/2がスレッショルトレベル。+5V系を直結すると壊れるので、直列に1KΩを接続するか、2SC1815で反転レベルシフト入力
  • ディジタル入出力ポートの総数
    28ビット。Propeller全32ビットのうち、書き込みインターフェースに2本、外部フラッシュFFPROMに2本を使うので、残りは28本
  • アナログ入力ポートの電圧(5Vか3.3Vか)
    専用アナログ入力ピンは無い。RCタイプで作れば+3.3V系となる
  • アナログ入力ポートの総数
    専用アナログ入力ピンは無い。RCタイプで作れば1入力に2ポートを使用する。外部ディジタルA/Dチップからのディジタル入力が推奨
  • アナログ出力に関して(PWM/電圧)
    出力ポートにアセンブラでPWM制御すればディジタル出力の最大28チャンネルでPWM出力可能。あるいはポートのビット数が多いので外付けD/Aに出す。2ポートを使ってオーディオD/A出力しているサンプルも提供されている
  • MIDI入力増設法
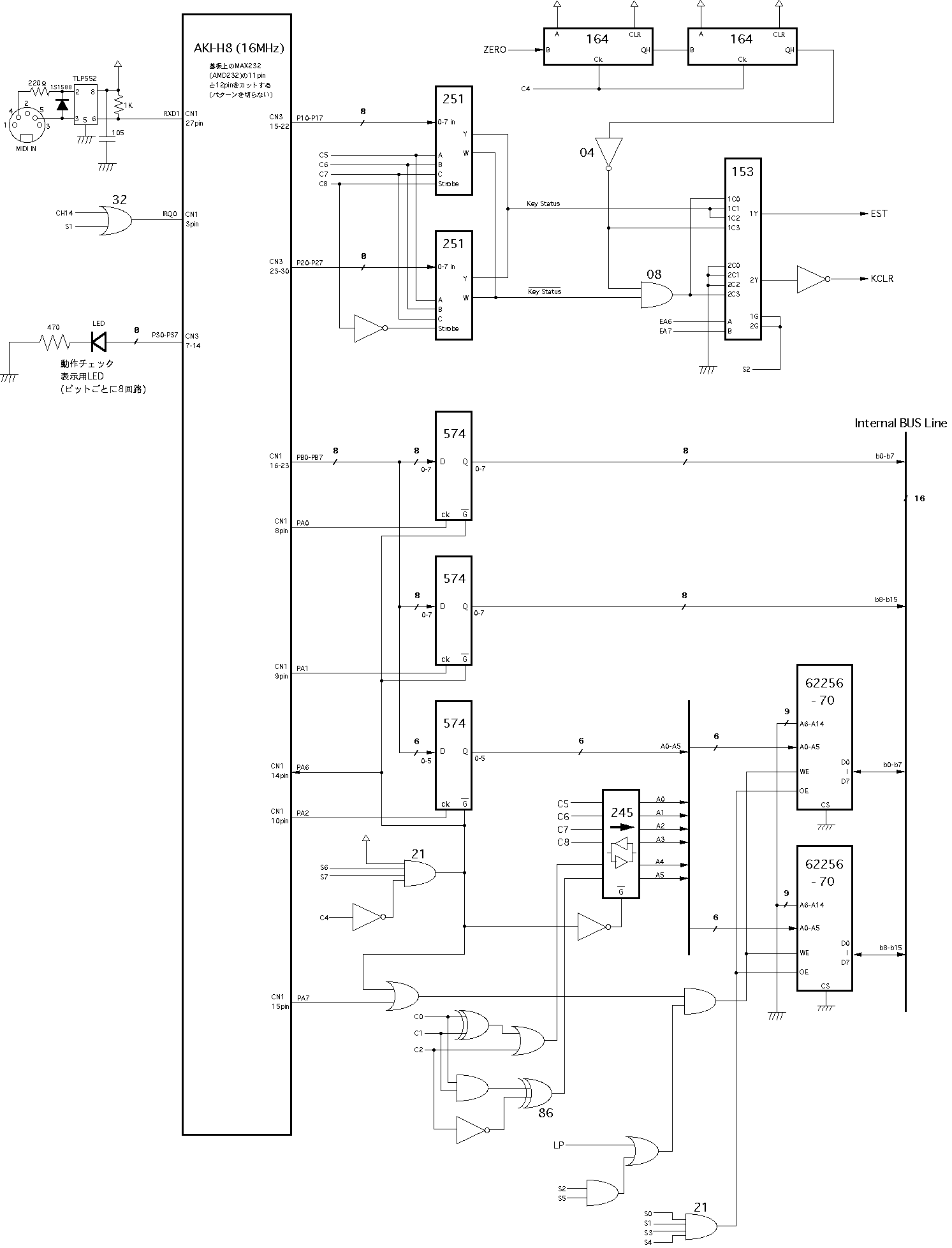
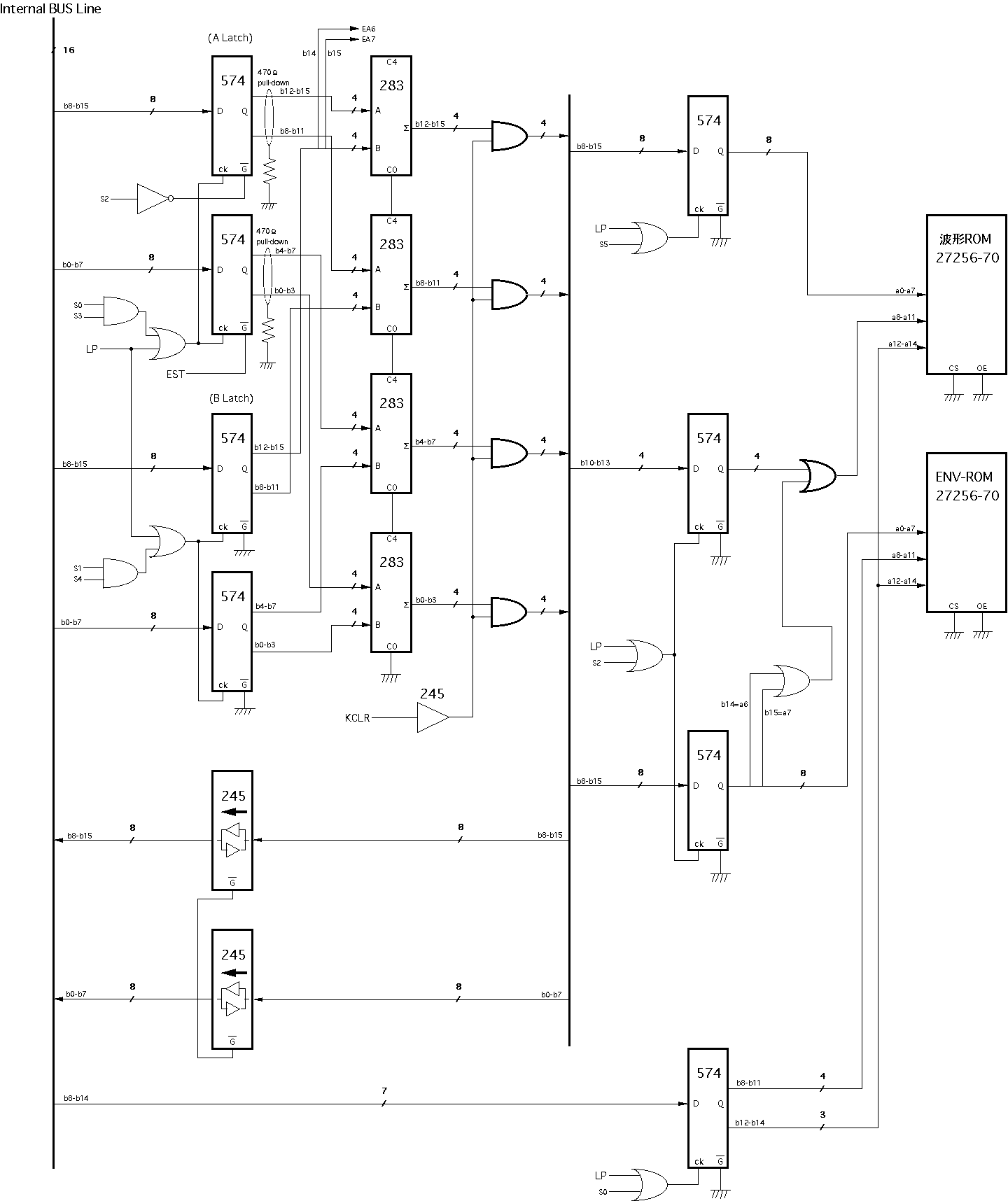
    Propeller日記(3)あたりで公開した、オリジナルMIDI入力回路/ドライバでMIDI入力に完全対応。TLP552との接続に2SC1815を使う(論理反転しているので注意)
  • MIDI出力増設法
    Propeller日記(3)あたりで公開した、オリジナルMIDI出力回路/ドライバでMIDI出力に完全対応。74HC05との接続に2SC1815を使う(論理反転しているので注意)
  • シリアル入出力増設の対応(→XBee接続)と信号電圧(+5Vか+3.3Vか)
    空いているピンとCogで何ポートでもシリアル増設可能(MIDIと両方もOK)。XBeeは+3.3Vなので直結可能。+5V系のシリアルではレベルシフトが必要
  • ビンは定義されているが回路としては「NC」となる信号(回路設計CADの身配線エラー対策)
    以下のピンはボード上の回路の信号が出ているが使わないので「NC」指定が必要
    • 30ピン XI
    • 31ピン XO
    • 37ピン P28 EEPROM用
    • 38ピン P29 EEPROM用
    • 39ピン P30 USB通信用
    • 40ピン P31 USB通信用
  • 総ピン数
    40ピン
  • 外形寸法、mil幅、ビン配置/定義の図面
    40ピンDIPのPropellerと同一の600mil-DIPなので、Propellerデータシートから作った以下を提示する

・・・こんなところだろうか。 近鉄アーバンライナーは名古屋から2時間で、もう鶴橋である。とりあえず今日の進展としては十分かな(^_^)。

2012年9月23日(日)

Gabriel Solis氏の造語　(Improvisation vs Composition)
Mind: "Comprovisation" and "Improvosed" Music

Production of Form --- Practice of Freedom --- の弁証法的ループ
("Improvosed" Music) --- ("Comprovisation" Music) --- という事

Creativity, Repetition and Immitation

上のメモは謎のままとして(^_^;)、日本音楽即興学会(JASMIM)が終了して、 新神戸から飲んだ「神戸ワイン」360mlが空いて、名古屋を過ぎて帰途はあと30分である。 学会では内職ナシで、なかなかに収穫があった。 無事に発表も終了した。大部分はどこかで見たスライドであるが(^_^;)、ブレゼンは これ である。 なんか異常にデカいのは、いつものように画像満載だからである。 ということで、この週末はここまで。

2012年9月24日(月)

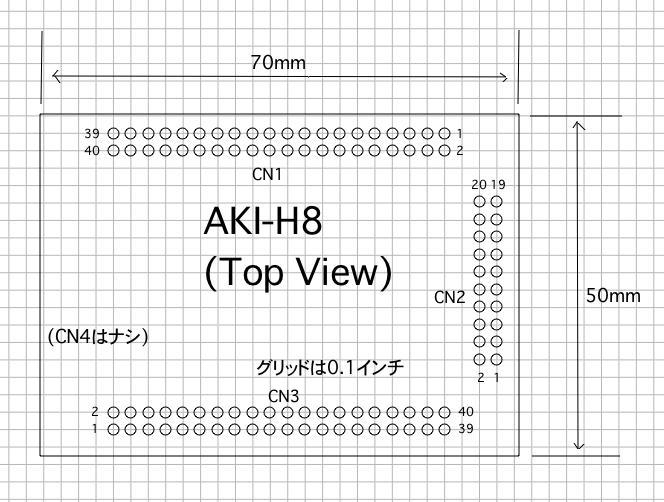
夏休みもあと1週間である。 来週の月曜日からは(もっとも後期は水曜日の1・2・4・5限に詰め込んでいるが)、いよいよ怒濤の季節となる。 今週は「嵐の前の静けさ」のように予定もないので、 AKI-H8 でも、Propellerクリップボードと同様に整理していくことにした。 AKI-H8は、多数のピンに日立「H8/3048F」のピンをそのまま出している。 上のように、だいぶ昔、1999年の 作るサウンドエレクトロニクス より前に、初めて秋月電子でAKI-H8の開発ボードのキットを買った時に付録していたCDROMから、 「H8/3048Fマニュアル」のPDFを発掘してきた。 これは、分厚い2冊の日立のマニュアルを全ページ、スキャンしてPDF化したという荒技(^_^;)だが、 たぶん秋月がこのデータを配布しているのは、日立のOKがあっての事なのだろう。
  • AKI-H8
  • 電源供給(+5Vか+3.3VかACアダプタ[5-9V]か)
    +5V供給がbest。オンボードに6-9V用の3端子レギュレータはあるが、それをパスして+5Vラインの直結推奨
  • リセット(負論理でSW経由でGNDショートでOK?)
    GNDへのショートでOK
  • 書き込み手法(オンボードコネクタ?)
    基板の4辺にあるコネクタのうち、CN1からCN3までの3個は基板の下に普通に2列ピンヘッダ(オス)で出すが、書き込みポートのあるCN4(10ピン)だけは、基板の上に2列10ピンのピンヘッダ(オス)で出す。ここに自作のAKI-H8ライタを接続してファームウエェアを書き込む。この際には+9Vが"Power"ラインにかかるので注意。書き込み時にはシステムの+5Vラインは生かしておくこと
  • ディジタル出力ポートの電圧(+5Vか+3.3Vか)
    +5V
  • ディジタル出力ポートの電流ドライブ能力(LED直接ドライブの可否)
    ポート「1,2,5,B」が10mA、それ以外のポートは2mA。ドライバは必須
  • ディジタル入力ポートの電圧(+5Vか+3.3Vか)
    +5V。CMOSなのでスレショルドは2.5V
  • ディジタル入出力ポートの総数
    「靄夜」の経験から、最大で64ビットは外部増設回路ナシに出力可能。マニュアルによれば、8ビットの汎用入出力ポートがP1,P2,P3,P4,PA.PB、4ビットの汎用入出力ポートがP5、7ビットの汎用入出力ポートがP6、(A/Dと兼用なのでP7はパス)、5ビットの汎用入出力ポートがP8、(USARTと兼用なのでP9はパス)、これらを合計すると48+4+7+5=64
  • アナログ入力ポートの電圧(5Vか3.3Vか)
    5V系。外部にシグナルコンディショニングのLM324などを付けると0-4V程度になる
  • アナログ入力ポートの総数
    8ビット精度のA/D入力ポートが8チャンネル
  • アナログ出力に関して(PWM/電圧)
    「靄夜」の手法で、最大64ポートの全てをPWMアナログ(LED連続値点灯制御)は容易。これと別にアナログ電圧出力が2ビットあり
  • MIDI入力増設法
    ここにあるように、ボード上のRS232CインターフェースICの11/12番ピンをカットする。あとはここにあるように、この回路でOK(動作確認用LEDのCN1-23pinはナシ)
  • MIDI出力増設法
    ここにあるように、ボード上のRS232CインターフェースICの11/12番ピンをカットする。あとはここにあるように、この回路でOK
  • シリアル入出力増設の対応(→XBee接続)と信号電圧(+5Vか+3.3Vか)
    MIDIとの共存は出来ないが、ここにあるように、ボード上のRS232CインターフェースICの11/12番ピンをカットすれば、+5V系としてUSARTを利用可能。XBeeの場合にはレベルシフトが必要
  • ビンは定義されているが回路としては「NC」となる信号(回路設計CADの身配線エラー対策)
    以下のピンはボード上の回路の信号が出ているが使わないので「NC」指定が必要
    • I/Oポートで最終的にシステムに使用しないピン全て
    • コネクタ1の39/40ピン 電源7805入力 ※+5Vを直接供給する
    • コネクタ2の3ピン STBY
    • コネクタ2の5ピン NMI
    • コネクタ3の38ピン CK
  • 総ピン数
    40+40+20=100ピン
  • 外形寸法、mil幅、ビン配置/定義の図面
    秋月電子では、PDF等でAKI-H8の外形寸法図などの情報を公開していない。秋月サイトの写真とともにとりあえず作ったのが、以下である

このようにAKI-H8を改めて整理して眺めてみると、DMAとかスマートカードとか、 豊富な機能のうちまったく使ったこともない部分がとても多いことに気付いた。 これまで多数のシステムにAKI-H8を使ってきたが、まだまだ使いこなし/使い倒したわけでもなかったのだ。 まぁ、汎用組み込みマイコンなんて、そういうものかもしれない。

さて、引き続き、Arduino Nanoについても調べてみることにした。 2010年の メディアアートシンポジウム の 「フィジカル・コンピューティング」ワークショップ の時に、僕はMaxとGainerの紹介を担当したが、 小林さんのパートの教材として赤外線距離センサ2個と2軸ジョイスティックとLED3個を繋いだ以下のようなものを10個ほど作っていたが、 これが既にArduino Nanoだった。(^_^;)

ただしよく見ると、上の写真のNano(V3.0)は、 この写真のNano(V2.2) とはまったく外見が違っている(^_^;)。 まさかスペックは(上位)互換だと思うが、ここも調べてみる必要がありそうだ。

いつものように Arduinoのサイト に行き、 Hardware のページの中で、 Arduino Nano のページに行き、既にゲットしていた これ はV3.0の回路図だった事を確認した上で、 Arduinoマニュアル(V2.3) をゲットした。

The Arduino Nano is a small, complete, and breadboard-friendly board based on the ATmega328 (Arduino Nano 3.0) or ATmega168 (Arduino Nano 2.x). It has more or less the same functionality of the Arduino Duemilanove, but in a different package. It lacks only a DC power jack, and works with a Mini-B USB cable instead of a standard one. The Nano was designed and is being produced by Gravitech.
ということで、CPUが16ビットから32ビットのATmega328になっただけで、図面的には Arduinoマニュアル(V2.3) を適用して、以下を整理してみた。
  • Arduino Nano
  • ※1ピンはミニUSBコネクタとは反対側なので向きと位置に注意すること
  • 電源供給(+5Vか+3.3VかACアダプタ[5-9V]か)
    VIN端子に6-20V(7-12V推奨)を供給すると内部+5Vを外部にも出せる。ただしオンボードのFTDIインターフェースICはUSB接続している時にだけUSBバスパワーで動作するので、スタンドアロンでVINとか+5Vを受けた場合には、+3.3V出力は出てこないらしい(本当?)
  • リセット(負論理でSW経由でGNDショートでOK?)
    GNDへのショートでOK。オンボードのResetスイッチあり(GNDとショートする)
  • 書き込み手法(オンボードコネクタ?)
    ボード上のミニUSBコネクタでそのまま書き込みOK
  • ディジタル出力ポートの電圧(+5Vか+3.3Vか)
    +5V
  • ディジタル出力ポートの電流ドライブ能力(LED直接ドライブの可否)
    各ポートごとに+5Vで40mA
  • ディジタル入力ポートの電圧(+5Vか+3.3Vか)
    +5V。CMOSなのでスレショルドは2.5V
  • ディジタル入出力ポートの総数
    D0/D1はUSBシリアル通信に使用するので、残りはD2からD13までの12ビット
  • アナログ入力ポートの電圧(5Vか3.3Vか)
    5V系。外部にシグナルコンディショニングのLM324などを付けると0-4V程度になる
  • アナログ入力ポートの総数
    10ビット精度のA/D入力ポートが8チャンネル
  • アナログ出力に関して(PWM/電圧)
    ディジタル入出力12ビットのうち、「PWM: 3, 5, 6, 9, 10, and 11. Provide 8-bit PWM output with the analogWrite() function. 」ということで6チャンネルのPWM出力が可能
  • MIDI入力増設法
    「Arduino日記」に書いたように、Cでプログラミングした場合には、MIDIデータを取りこぼすので「使えない」(^_^;)
  • MIDI出力増設法
    「Arduino日記」に書いたように、MIDI出力は使える。ジャミーズ娘+では、Arduinoが活躍している
  • シリアル入出力増設の対応(→XBee接続)と信号電圧(+5Vか+3.3Vか)
    USBポートとMIDIですら共用なので、他に増設は無理
  • ビンは定義されているが回路としては「NC」となる信号(回路設計CADの身配線エラー対策)
    ナシ。30ピン全てが定義され接続される
  • 総ピン数
    30ピン
  • 外形寸法、mil幅、ビン配置/定義の図面
    Propeller等と同一の600mil-DIP。ただし30ピン、さらにその両側に1つずつ、4隅に単なる穴があるので注意

これで残る登場人物はGainerである。 Gainerだけは他の3つのマイコンと違って、スタンドアロンでなく、ホストPC側にMaxとかFlashなどが走ることになる。 そして、I/Oピンが4*4=16ビットしかないので、ファームウェアとして持っているいくつものモードから切り換えて使用する。 この汎用実験基板に搭載するには、そのあたりを他の3種のマイコンとどう摺り合わせるか、 というのが、おそらく設計上の最大の「腕の見せ所」である。 明日は、東京デザイナーズウイークに出展するという3回生4人からのアポだけなので、 Gainerも進めて、基板設計の全体像を目標にしてみよう。

2012年9月25日(火)

前夜はDVD鑑賞に燃えた。 届いたばかりのMJのDVD「ライヴ.アット.ウェンブリ. 7.16.1988」を観たが、 いやー、良かった(^_^)。 mixiの日記(友人限定)に思わず以下のように紹介した。 
これは「買い」のDVD

AKBとかの学芸会芸能人は流石に恥ずかしくなるでしょう。これ観たら。

マイケル・ジャクソン DVD
ライヴ.アット.ウェンブリ. 7.16.1988

凄く良かったです(^_^)
This is Itも凄いけど、これは25年前、まさに全盛期のMJが同じ曲をやってます。
キレてます。お奨めです。

ホーナストラックの横浜アリーナでのMJコンサートの客席の日本人が、
いやー「昭和」でしたが。(^_^;)

・・・しかし、MJと僕は同い年なのであった。山口百恵も同級生なのであった。(^_^;)

午前中には、アポのあったメディア造形の田中さん他3人(空間1人・生産2人)が研究室に来たが、 あと1ヶ月ほどで出展するというインスタレーション作品の制作に対するプロジェクトマネジメントの甘さが凄かった。 センサ等をサッサと仕込めば、純然たる造形作品よりも簡単に作品が作れる、 と思うその誤解は、こちら教員にも原因があるのかもしれない。 マルチメディア室に行って、かつて ここ にある小畑さんの作品「海潮音」のために製作した、以下の5チャンネル・ソレノイド駆動システム(Gainer)を貸し出す、 という事になったが、これからの制作が順調に進まないと、構想した作品を実現するのはなかなか大変である。

そして午後になって、懸案だった「科研費」を調べてみた。 応募したいのはやまやまだが、なんせあの書類の山に閉口してしまう。 2時間ほどかけて久しぶりに書類PDFを見たが、ゲンナリしてしまった。 いずれ再度、挑戦してみようか。

そして、注文していた PropQuickStart が以下のように届いた。 なかなか可愛いボードである。

しかし以下のように、今回の実験試作基板のサイズとして想定しているユバーサル基板の上にさらに並べてみると、 ちょっと窮屈である。やっぱりこれを搭載するのは無理かなぁ。

さて、懸案のGainer回りの検討に入ることが出来ないまま夕方になってしまった。 Gainerについては、小林さんの 公式サイト にも、もちろん 解説ページ があり、ここに電気的なスペックとかが載っている。 ただし「パッと見」には、Gainer miniを製造している この会社 の このPDFの表 が便利なので、ここではこちらを使うことにした。 8つのコンフィギュレーションのうち、「7」と「8」は特殊なので除外して、6つのコンフィギュレーションがあるが、いずれにおいても「アナログ出力」というのは、 実はPWMのディジタル出力である。外部D/Aに出すにはピンが少ないので、ここが「汎用」という時のGainerの最大の弱点である。 以下の整理においては、なるべく最大機能で使えるように、それぞれコンフィギュレーションを変更する、と規定している。
  • Gainer
  • 電源供給(+5Vか+3.3VかACアダプタ[5-9V]か)
    USBから供給の+5V系。スタンドアロンでなくホストとのUSB接続が前提なので。一応オンボード・レギュレーションの+3.3V出力がある
  • リセット(負論理でSW経由でGNDショートでOK?)
    GNDへのショートでOK。オンボードのResetスイッチあり(GNDとショートする)
  • 書き込み手法(オンボードコネクタ?)
    ボード上のミニUSBコネクタでそのまま書き込みOK
  • ディジタル出力ポートの電圧(+5Vか+3.3Vか)
    +5V
  • ディジタル出力ポートの電流ドライブ能力(LED直接ドライブの可否)
    各ポートごとに+5Vで25mA(吸い込み)、ただし全部の合計が150mA。供給電流の場合にはポートごと10mAで合計80mAまで
  • ディジタル入力ポートの電圧(+5Vか+3.3Vか)
    +5V。CMOSなのでスレショルドは2.5V
  • ディジタル入出力ポートの総数
    ディジタル出力ポート数を最大にするコンフィギュレーション[6]で16ビット出力。ディジタル入力ポート数を最大にするコンフィギュレーション[5]で16ビット入力(内部pull-down)。混在の場合にはアナログ入出力もあるコンフィギュレーション[1]で4ビット出力/4ビット入力が最大。ラッチ/マルチプレクサで多重化するにも苦しい(^_^;)
  • アナログ入力ポートの電圧(5Vか3.3Vか)
    5V系。コンフィギュレーション[1]-[4]では、「アナログ入力用可変ゲインアンプ：最大48倍（16段階）」を使える(使ったこと無いケド)
  • アナログ入力ポートの総数
    アナログ入力ポート数を最大にするコンフィギュレーション[2][4]で8チャンネル入力。ただし4チャンネルのコンフィギュレーション[1][3](サンプリング　220Hz)に比べて、サンプリング140Hzと低速になる
  • アナログ出力に関して(PWM/電圧)
    1KHz分解能のアナログPWM出力に対応しているのは、コンフィギュレーション[1][2]が4チャンネル、コンフィギュレーション[3][4]が8チャンネル
  • MIDI入力増設法
    GainerでMIDI通信は無理(^_^;)
  • MIDI出力増設法
    GainerでMIDI通信は無理(^_^;)
  • シリアル入出力増設の対応(→XBee接続)と信号電圧(+5Vか+3.3Vか)
    Gainerでシリアル通信は無理(^_^;)
  • ビンは定義されているが回路としては「NC」となる信号(回路設計CADの身配線エラー対策)
    ナシ。28ピン全てが定義され接続される
  • 総ピン数
    28ピン
  • 外形寸法、mil幅、ビン配置/定義の図面
    オリジナルのGainerを作っているsparkfunの資料から、以下である。 オリジナルのGainerとは、ビン間が0.1インチで14ピン2列、というのはピン互換だが、基板全体として2列の間隔が異なっているので注意が必要である

どうもここまでは、ネットで見つけた「Gainer mini」を想定しつつも、手元にはオリジナルのGainerしか無かった、 という状況を初めて理解した(^_^;)。 Gainerは28ピンでも2列の間隔がかなり広い(1インチ?)が、上の図からは、Gainer miniはそれより狭いものの、 通常のDIPの600mil(2列の間隔が0.6インチ)よりもやや広い(0.7インチ?)気もする。 現物を注文してみたので、届いたら計測して上の図を補強することにした。 この日記も既に100kBを越えているので、ここを区切りとして、次は「続・Propeller日記(4)」としていこう。

続・Propeller日記(4) へ

「日記」シリーズ の記録